Giải mục 5 trang 103, 104 SGK Toán 11 tập 2 - Cánh Diềua) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song (left( P right),left( Q right)). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
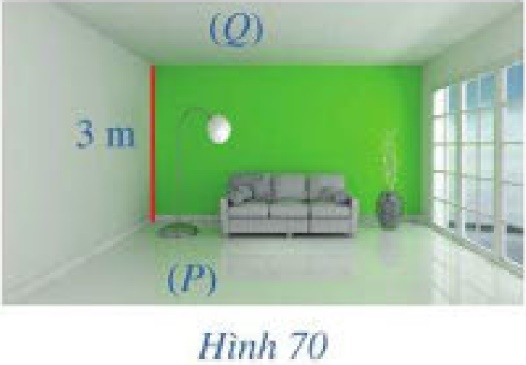
Hoạt động 4 a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song \(\left( P \right),\left( Q \right)\). Chiều cao của căn phòng là 3 m. Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song \(\left( P \right),\left( Q \right)\)?
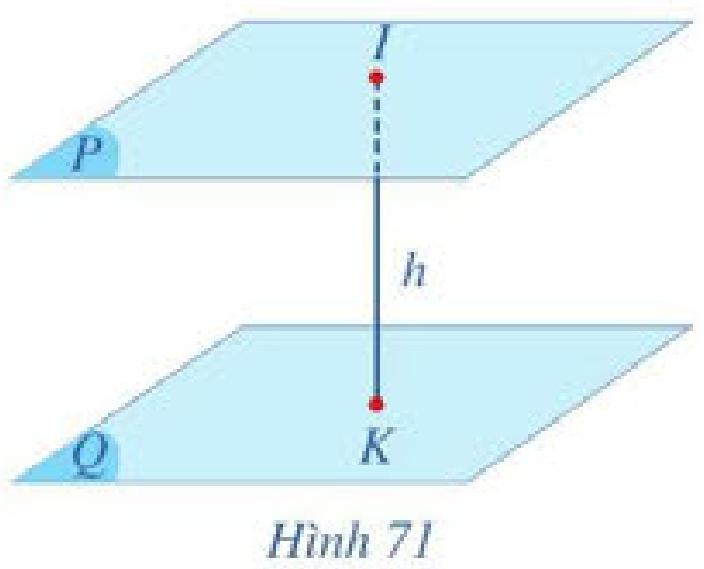
b) Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Xét điểm \(I\) tuỳ ý trong mặt phẳng \(\left( P \right)\), lấy \(K\) là hình chiếu của \(I\) trên \(\left( Q \right)\) (Hình 71). Khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) có phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\) hay không? Vì sao?
Phương pháp giải: Sử dụng tính chất của hai mặt phẳng song song. Lời giải chi tiết: a) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai mặt phẳng song song. b)
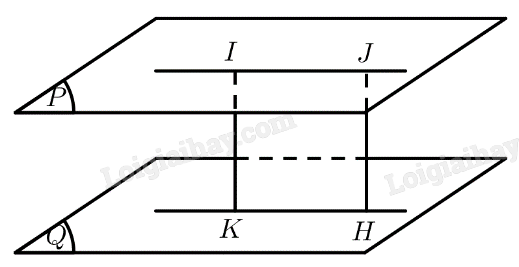
Trên mặt phẳng \(\left( P \right)\) lấy điểm \(J\) khác \(I\). Kẻ \(JH \bot \left( Q \right)\left( {H \in \left( Q \right)} \right)\) \( \Rightarrow HKIJ\) là hình chữ nhật \( \Rightarrow IK = JH\) \( \Rightarrow d\left( {I,\left( Q \right)} \right) = d\left( {J,\left( Q \right)} \right)\) Vậy khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) không phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\). Luyện tập 4 Cho hình lăng trụ \(ABC.A'B'C'\) có cạnh bên bằng \(a\), góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^ \circ }\). Tính khoảng cách giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\). Phương pháp giải: Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách từ một điểm trên mặt phẳng này đến mặt phẳng còn lại. Lời giải chi tiết:
Gọi \(H\) là hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\) \(\begin{array}{l} \Rightarrow A'H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA',\left( {ABC} \right)} \right) = \left( {AA',AH} \right) = \widehat {A'AH}\end{array}\) \(\Delta AA'H\) vuông tại \(H \Rightarrow A'H = AA'.\sin \widehat {A'AH} = \frac{{a\sqrt 3 }}{2}\) Vì \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\) nên: \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'H = \frac{{a\sqrt 3 }}{2}\)
|





















Danh sách bình luận