Giải mục 3 trang 33, 34, 35 SGK Toán 12 tập 2 - Kết nối tri thứcLập phương trình tổng quát của mặt phẳng Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
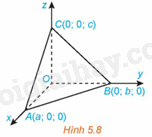
HĐ5 Trả lời câu hỏi Hoạt động 5 trang 33 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Dựa vào HĐ4, hãy nêu phương trình của \(\left( \alpha \right)\). Phương pháp giải: Sử dụng kiến thức về phương trình tổng quát của mặt phẳng để giải: Trong không gian Oxyz, mỗi phương trình \(Ax + By + Cz + D = 0\) (các hệ số A, B, C không đồng thời bằng 0) xác định một mặt phẳng nhận \(\overrightarrow n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến. Lời giải chi tiết: Gọi điểm M(x; y; z) thuộc \(\left( \alpha \right)\). Khi đó, hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau. Ta có: \(\overrightarrow {{M_o}M} \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\). Suy ra phương trình của \(\left( \alpha \right)\) là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\) \( \Leftrightarrow Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\). Vậy phương trình của \(\left( \alpha \right)\) là: \(Ax + By + Cz - A{x_0} - B{y_0} - C{z_0} = 0\). LT6 Trả lời câu hỏi Luyện tập 6 trang 33 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) và vuông góc với trục Oz. Phương pháp giải: Sử dụng kiến thức về phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến để viết phương trình: Trong không gian Oxyz, nếu mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\) thì có phương trình là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0 \Leftrightarrow Ax + By + Cz + D = 0\) với \(D = - \left( {A{x_0} + B{y_0} + C{z_0}} \right)\). Lời giải chi tiết: Vì mặt phẳng \(\left( \alpha \right)\) vuông góc với trục Oz nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n \left( {0;0;1} \right)\) làm một vectơ pháp tuyến. Mà mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {1;2; - 4} \right)\) nên phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\) là: \(0\left( {x - 1} \right) + 0\left( {y - 2} \right) + 1.\left( {z + 4} \right) = 0 \Leftrightarrow z + 4 = 0\). HĐ6 Trả lời câu hỏi Hoạt động 6 trang 33 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và biết cặp vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow v = \left( {a';b';c'} \right)\). a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\). b) Viết phương trình mặt phẳng \(\left( \alpha \right)\). Phương pháp giải: Sử dụng kiến thức về phương trình mặt phẳng đi qua một điểm và biết vectơ pháp tuyến để viết phương trình: Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\) thì có phương trình là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0 \Leftrightarrow Ax + By + Cz + D = 0\) với \(D = A{x_0} - B{y_0} - C{y_0}\). Lời giải chi tiết: a) Vì \(\overrightarrow u ,\overrightarrow v \) là các vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\). Do đó, \(\overrightarrow u ,\overrightarrow v \) cùng vuông góc với vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\). Một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) là: \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\). b) Vì mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\) và đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) nên phương trình mặt phẳng \(\left( \alpha \right)\) là: \(\left( {bc' - b'c} \right)\left( {x - {x_0}} \right) + \left( {ca' - c'a} \right)\left( {y - {y_0}} \right) + \left( {ab' - a'b} \right)\left( {z - {z_0}} \right) = 0\). LT7 Trả lời câu hỏi Luyện tập 7 trang 34 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2; - 1} \right),B\left( {4;1;2} \right),C\left( {2;3;1} \right)\). Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC. Phương pháp giải: Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau: + Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). + Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến\(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). Lời giải chi tiết: Trục Oy có một vectơ chỉ phương là: \(\overrightarrow j = \left( {0;1;0} \right)\). Đường thẳng BC có một vectơ chỉ phương là: \(\overrightarrow {BC} \left( { - 2;2; - 1} \right)\). Vì mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(A\left( {1; - 2; - 1} \right)\) đồng thời song song với trục Oy và đường thẳng BC nên mặt phẳng \(\left( \alpha \right)\) nhận \(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right]\) làm một vectơ pháp tuyến. \(\overrightarrow n = \left[ {\overrightarrow {BC} ,\overrightarrow j } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\0&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&2\\0&1\end{array}} \right|} \right) = \left( {1;0; - 2} \right)\) Do đó, phương trình mặt phẳng \(\left( \alpha \right)\) là: \(1\left( {x - 1} \right) - 2\left( {z + 1} \right) = 0 \Leftrightarrow x - 2z - 3 = 0\). HĐ7 Trả lời câu hỏi Hoạt động 7 trang 34 SGK Toán 12 Kết nối tri thức Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1;2;3} \right),B\left( { - 1;3;4} \right),C\left( {2; - 1;2} \right)\). a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC). b) Viết phương trình mặt phẳng (ABC). Phương pháp giải: Sử dụng kiến thức về lập phương trình mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi qua điểm M và biết cặp vectơ chỉ phương \(\overrightarrow u ,\overrightarrow v \) có thể thực hiện theo các bước sau: + Tìm vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). + Lập phương trình tổng quát của mặt phẳng đi qua M và biết vectơ pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow u ,\overrightarrow v } \right]\). Lời giải chi tiết: a) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\). b) Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - 2;1;1} \right),\overrightarrow {AC} \left( {1, - 3; - 1} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\). Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&1\\{ - 3}&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 1}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&1\\1&{ - 3}\end{array}} \right|} \right) = \left( {2; - 1;5} \right)\). Mặt phẳng (ABC) đi qua điểm \(A\left( {1;2;3} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1;5} \right)\) nên phương trình mặt phẳng (ABC) là: \(2\left( {x - 1} \right) - \left( {y - 2} \right) + 5\left( {z - 3} \right) = 0 \Leftrightarrow 2x - y + 5z - 15 = 0\). LT8 Trả lời câu hỏi Luyện tập 8 trang 35 SGK Toán 12 Kết nối tri thức (H.5.8) Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right)\) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) \(\left( {a,b,c \ne 0} \right)\).
Chứng minh rằng mặt phẳng \(\left( \alpha \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (Phương trình trên được gọi là phương trình mặt phẳng theo đoạn chắn). Phương pháp giải: Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau: + Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \). + Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\). + Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \). Lời giải chi tiết: Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - a;b;0} \right),\overrightarrow {AC} \left( { - a;0;c} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\). Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}b&0\\0&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - a}\\c&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - a}&b\\{ - a}&0\end{array}} \right|} \right) = \left( {bc;ac;ab} \right)\). Mặt phẳng (ABC) đi qua điểm A(a; 0; 0) và vectơ pháp tuyến \(\overrightarrow n = \left( {bc;ac;ab} \right)\) nên phương trình mặt phẳng (ABC) là: \(bc\left( {x - a} \right) + acy + abz = 0 \Leftrightarrow bcx + acy + abz = bca \Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (đpcm). VD2 Trả lời câu hỏi Vận dụng 2 trang 35 SGK Toán 12 Kết nối tri thức Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra. a) Xác định tọa độ của vị trí \({M_1},{M_2},{M_3}\) của vật tương ứng với các thời điểm \(t = 0,t = \frac{\pi }{2},t = \pi \). b) Chứng minh rằng \({M_1},{M_2},{M_3}\) không thẳng hàng và viết phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\). c) Vị trí \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) có luôn thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) hay không? Phương pháp giải: Sử dụng kiến thức về lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng để viết: Trong không gian Oxyz, bài toán viết phương trình mặt phẳng đi ba điểm không thẳng hàng A, B, C có thể thực hiện theo các bước sau: + Tìm cặp vectơ chỉ phương \(\overrightarrow {AB} ,\overrightarrow {AC} \) + Tìm vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\). + Lập phương trình tổng quát của mặt phẳng đi qua A và biết vectơ pháp tuyến là \(\overrightarrow n \). Lời giải chi tiết: a) Với \(t = 0\) ta có: \({M_1}\left( {1;1;1} \right)\). Với \(t = \frac{\pi }{2}\) ta có: \({M_2}\left( { - 1;1;0} \right)\). Với \(t = \pi \) ta có: \({M_3}\left( { - 1; - 1; - 1} \right)\). b) Hai vectơ \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) không cùng phương nên ba điểm \({M_1},{M_2},{M_3}\) không thẳng hàng. c) Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có cặp vectơ chỉ phương \(\overrightarrow {{M_1}{M_2}} \left( { - 2;0; - 1} \right),\overrightarrow {{M_1}{M_3}} \left( { - 2; - 2; - 2} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right]\). Ta có: \(\overrightarrow n = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 1}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{ - 2}\\{ - 2}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 2}&0\\{ - 2}&{ - 2}\end{array}} \right|} \right) = \left( { - 2; - 2;4} \right)\). Mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) có vectơ pháp tuyến \(\overrightarrow n \left( { - 2; - 2;4} \right)\) và đi qua điểm \({M_2}\left( { - 1;1;0} \right)\) nên phương trình mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\) là: \( - 2\left( {x + 1} \right) - 2\left( {y - 1} \right) + 4z = 0 \Leftrightarrow x + 1 + y - 1 - 2z = 0 \Leftrightarrow x + y - 2z = 0\) (1) c) Với \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thay vào (1) ta có: $\cos t-\sin t+\cos t+\sin t-2\cos t=0\Leftrightarrow 0=0\left( L D\right)$. Vậy \(M\left( {\cos t - \sin t,\cos t + \sin t,\cos t} \right)\) thuộc mặt phẳng \(\left( {{M_1}{M_2}{M_3}} \right)\). Do đó, vật thể M luôn chuyển động trong một mặt phẳng cố định.
|




















Danh sách bình luận