Bài tập trắc nghiệm trang 218, 219 SBT đại số và giải tích 11Giải bài tập trắc nghiệm trang 218, 219 sách bài tập đại số và giải tích 11 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Chọn đáp án đúng: 5.124 Đạo hàm của hàm số y = x3 - 2x2 + x + 1 tại x = 0 bằng A. 1 B. 0 C. 2 D. -2 Lời giải chi tiết: \(\begin{array}{l}y' = 3{x^2} - 4x + 1\\y'\left( 0 \right) = 3.0 - 4.0 + 1 = 1\end{array}\) Chọn đáp án: A 5.125 Hàm số \(y = \left\{ \begin{array}{l}2x\,voi\,x \ge 0\\ - 3x\,voi\,x < 0\end{array} \right.\) không có đạo hàm tại A. x = 2 B. x = 1 C. x = 0 D. x = -1 Lời giải chi tiết: Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}}= \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{2x - 0}}{{x - 0}} = 2\\\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ - 3x - 0}}{{x - 0}} = - 3\end{array}\) \( \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}}\) \( \ne \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{y\left( x \right) - y\left( 0 \right)}}{{x - 0}}\) \( \Rightarrow \) Hàm số không có đạo hàm tại \(x = 0\). Chọn đáp án: C 5.126 Phương trình tiếp tuyến với đồ thị của hàm số y = x3 + 1 tại x = -1 là A. y = 3x + 2 B. y = 3x - 2 C. y = 3x + 4 D. y = 3x + 3 Lời giải chi tiết: Ta có: \(y' = 3{x^2}\) \( \Rightarrow y'\left( { - 1} \right) = 3\) \({x_0} = - 1 \Rightarrow y\left( { - 1} \right) = 0\) Phương trình tiếp tuyến \(y = 3\left( {x + 1} \right) + 0\) hay \(y = 3x + 3\). Chọn đáp án: D 5.127 Đạo hàm của hàm số \(y = \dfrac{{2x}}{{\sin x}}\) là
Lời giải chi tiết: \(\begin{array}{l}y' = \dfrac{{\left( {2x} \right)'\sin x - 2x\left( {\sin x} \right)'}}{{{{\sin }^2}x}}\\ = \dfrac{{2\sin x - 2x\cos x}}{{{{\sin }^2}x}}\\ = \dfrac{{2\sin x}}{{{{\sin }^2}x}} - \dfrac{{2x\cos x}}{{{{\sin }^2}x}}\\ = \dfrac{2}{{\sin x}} - \dfrac{{2x\cot x}}{{\sin x}}\\ = \dfrac{{2 - 2x\cot x}}{{\sin x}}\\ = \dfrac{{2\left( {1 - x\cot x} \right)}}{{\sin x}}\end{array}\) Chọn đáp án: B 5.128 Cho f(x) = x3/3 - 2x2 + m2x - 5. Tìm tham số m để f'(x) > 0 với mọi x ∈ R A. m > 2 B. m > 2 hoặc m < -2 C. m < -2 D. m ∈ R Lời giải chi tiết: \(f'\left( x \right) = {x^2} - 4x + {m^2}\) có \(\Delta ' = 4 - {m^2}\) Để \(f'\left( x \right) > 0,\forall x \in \mathbb{R}\) thì \(\left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = 4 - {m^2} < 0\end{array} \right.\) \( \Leftrightarrow 4 - {m^2} < 0\) \( \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\) Chọn đáp án: B 5.129 Cho f(x) = tan(2x3 - 5). Tìm f'(x)
Lời giải chi tiết: \(\begin{array}{l}f'\left( x \right)\\ = \left( {2{x^3} - 5} \right)'.\dfrac{1}{{{{\cos }^2}\left( {2{x^3} - 5} \right)}}\\ = 2.3{x^2}.\dfrac{1}{{{{\cos }^2}\left( {2{x^3} - 5} \right)}}\\ = \dfrac{{6{x^2}}}{{{{\cos }^2}\left( {2{x^3} - 5} \right)}}\end{array}\) Chọn đáp án: D 5.130 Tìm nghiệm của phương trình f''(x) = 0 biết f(x) = 3cosx - √3sinx A. x = π/6 + kπ B. x = π/4 + kπ C. x = π/3 + kπ D. x = kπ Phương pháp giải: HD: Tính f’’(x) rồi giải phương trình tanx = √3. Lời giải chi tiết: \(\begin{array}{l}f'\left( x \right) = - 3\sin x - \sqrt 3 \cos x\\f''\left( x \right) = - 3\cos x + \sqrt 3 \sin x\\f''\left( x \right) = 0\\ \Leftrightarrow - 3\cos x + \sqrt 3 \sin x = 0\\ \Leftrightarrow \sqrt 3 \sin x = 3\cos x\\ \Leftrightarrow \sin x = \sqrt 3 \cos x\\ \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} = \sqrt 3 \\ \Leftrightarrow \tan x = \sqrt 3 = \tan \dfrac{\pi }{3}\\ \Leftrightarrow x = \dfrac{\pi }{3} + k\pi ,k \in \mathbb{Z}\end{array}\) Chọn đáp án: C 5.131 Cho y = tan3x. Tìm dy
Lời giải chi tiết: \(\begin{array}{l}y' = 3{\tan ^2}x\left( {\tan x} \right)'\\ = 3{\tan ^2}x.\dfrac{1}{{{{\cos }^2}x}}\\ = 3.\dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}.\dfrac{1}{{{{\cos }^2}x}}\\ = \dfrac{{3{{\sin }^2}x}}{{{{\cos }^4}x}}\\ \Rightarrow dy = y'dx = \dfrac{{3{{\sin }^2}x}}{{{{\cos }^4}x}}dx\end{array}\) Chọn đáp án: A Loigiaihay.com
|














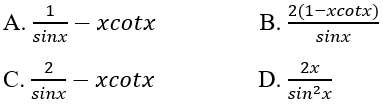
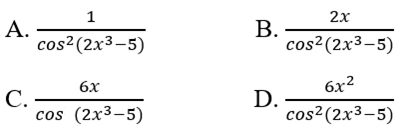
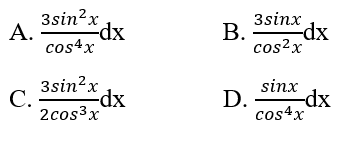






Danh sách bình luận