Giải bài tập 5 trang 20 SGK Toán 12 tập 2 - Chân trời sáng tạoMặt cắt ngang của một ống dẫn khí nóng là một hình vành khuyên như hình dưới đây. Khí bên trong ống được duy trì ở \({150^o}{\rm{C}}\). Biết rằng nhiệt độ \(T\left( {^oC} \right)\) tại điểm A trên thành ống là hàm số của khoảng cách \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) từ A đến tâm của mặt cắt và \(T'\left( x \right) = - \frac{{30}}{x}\) \(\left( {6 \le x \le 8} \right)\). Tìm nhiệt độ mặt ngoài của ống. Tổng hợp đề thi giữa kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
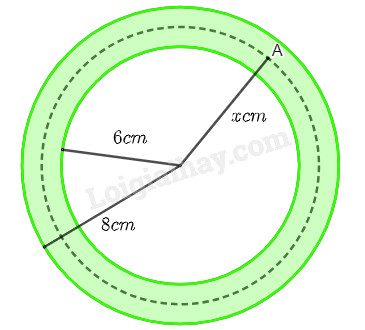
Đề bài Mặt cắt ngang của một ống dẫn khí nóng là một hình vành khuyên như hình dưới đây. Khí bên trong ống được duy trì ở \({150^o}{\rm{C}}\). Biết rằng nhiệt độ \(T\left( {^oC} \right)\) tại điểm A trên thành ống là hàm số của khoảng cách \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) từ A đến tâm của mặt cắt và \(T'\left( x \right) = - \frac{{30}}{x}\) \(\left( {6 \le x \le 8} \right)\). Tìm nhiệt độ mặt ngoài của ống.
Phương pháp giải - Xem chi tiết Do nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\). Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\). Lời giải chi tiết Do nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\). Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\). Ta có \(\int\limits_6^8 {T'\left( x \right)dx} = \int\limits_6^8 { - \frac{{30}}{x}dx} = - 30\int\limits_6^8 {\frac{1}{x}dx = - 30.\left. {\left( {\ln \left| x \right|} \right)} \right|_6^8 = - 30\ln 8 + 30\ln 6} \). Vậy nhiệt độ bên ngoài mặt ống là \(T\left( 8 \right) = - 30\ln 8 + 30\ln 6 + 150 \approx 141,{37^o}C\)
|




















Danh sách bình luận