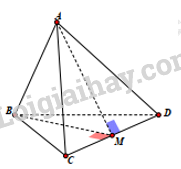
Giải bài tập 2.28 trang 73 SGK Toán 12 tập 1 - Kết nối tri thứcCho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng A. \(\frac{{{a^2}}}{4}\). B. \(\frac{{{a^2}}}{2}\). C. \(\frac{{{a^2}}}{3}\). D. \({a^2}\). Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Quảng cáo
Đề bài Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng Phương pháp giải - Xem chi tiết Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). Lời giải chi tiết
Tam giác ACD có ba cạnh bằng a nên tam giác ACD đều, AM là đường trung tuyến đồng thời là đường cao nên \(AM = \frac{{a\sqrt 3 }}{2}\). Tam giác CBD có ba cạnh bằng a nên tam giác CBD đều, BM là đường trung tuyến đồng thời là đường cao nên \(BM = \frac{{a\sqrt 3 }}{2}\). Áp dụng định côsin vào tam giác ABM ta có: \(\cos \widehat {BAM} = \frac{{A{M^2} + A{B^2} - M{B^2}}}{{2AB.MB}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.a}} = \frac{{\sqrt 3 }}{3}\) \(\overrightarrow {AB} .\overrightarrow {AM} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AM} } \right) = a.\frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{3} = \frac{{{a^2}}}{2}\) Chọn B  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
