Bài 97 trang 122 SBT toán 9 tập 1

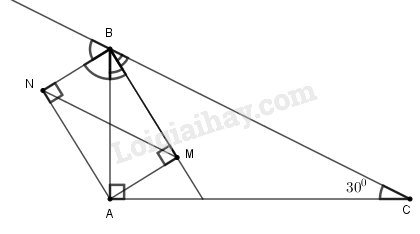
Đề bài

Cho tam giác \(ABC\) vuông ở \(A\), \(\widehat C = 30^\circ,\)\(BC = 10cm.\)

a) Tính \(AB, AC.\)

b) Từ \(A\) kẻ \(AM, AN\) lần lượt vuông góc với các đường phân giác trong và ngoài của góc \(B\).

Chứng minh: \(MN // BC\) và \(MN = AB.\)

c) Chứng minh hai tam giác \(MAB\) và \(ABC\) đồng dạng. Tìm tỉ số đồng dạng.

Lời giải chi tiết

a) Trong tam giác vuông \(ABC\), ta có:

\(AB = BC.\sin \widehat C = 10.\sin 30^\circ\)\(  = 10.\displaystyle {1 \over 2} = 5\,(cm)\)

\(AC = BC.\cos \widehat C = 10.\cos 30^\circ  \)\(= 10.\displaystyle {{\sqrt 3 } \over 2} = 5\sqrt 3 \,(cm)\)

b) Ta có:

\(BM \bot BN\) (hai tia phân giác của 2 góc kề bù thì vuông góc với nhau) \( \Rightarrow \widehat {MBN} = 90^\circ \,(1)\)

\(AM \bot BM\) (gt) \( \Rightarrow \widehat {AMB} = 90^\circ \,(2)\)

\(AN \bot BN\) (gt) \( \Rightarrow \widehat {ANB} = 90^\circ \,(3)\)

Từ (1), (2) và (3) suy ra tứ giác \(AMBN\) là hình chữ nhật.

Suy ra \(AM=BN, BM=AN, AB=MN\) (tính chất hình chữ nhật)

Suy ra: \(∆AMB = ∆NBM\) (c.g.c)

\(\Rightarrow \widehat {ABM} = \widehat {NMB}\)

Mà \(\widehat {ABM} = \widehat {MBC}\,(gt)\)

Suy ra: \(\widehat {NMB} = \widehat {MBC}\)

Suy ra \(MN // BC\) (có cặp so le trong bằng nhau)

Vì \(AMBN\) là hình chữ nhật nên \(AB = MN\).

c) Tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {ABC} + \widehat C = 90^\circ \)

Suy ra: \(\widehat {ABC} = 90^\circ  - \widehat C = 90^\circ  - 30^\circ  = 60^\circ \)

Suy ra: \(\widehat {ABM} = \displaystyle {1 \over 2}\widehat {ABC} = {1 \over 2}.60^\circ  = 30^\circ \)

Xét hai tam giác \(ABC\) và \(MAB\), ta có:

\(\widehat {BAC} = \widehat {AMB} = 90^\circ \)

\(\widehat {ACB} = \widehat {ABM} = 30^\circ \)

Suy ra \(∆ABC\) đồng dạng với \(∆MAB\) (g.g)

Tỉ số đồng dạng: \(k = \displaystyle {{AB} \over {BC}} = {5 \over {10}} = {1 \over 2}\)

Loigiaihay.com