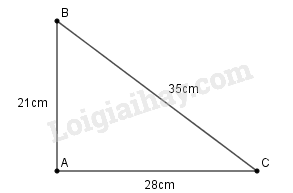
Bài 93 trang 121 SBT toán 9 tập 1

Đề bài

Cho tam giác \(ABC\). Biết : \(AB = 21cm\), \(AC = 28cm, BC = 35cm.\)

a) Chứng minh tam giác \(ABC\) vuông.

b) Tính sinB, sinC.

Lời giải chi tiết

a) Ta có: \(A{B^2} = {21^2} = 441\)

\(A{C^2} = {28^2} = 784\)

\(B{C^2} = {35^2} = 1225\)

Vì \(A{B^2} + A{C^2} = 441 + 784\)\( = 1225 = B{C^2}\)  nên tam giác \(ABC\) vuông tại \(A\) ( theo định lí đảo Pi-ta-go).

b) Xét tam giác ABC vuông tại A, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: 

\(\sin \widehat B = \displaystyle {{AC} \over {BC}} = {{28} \over {35}} = {4 \over 5} = 0,8\)

\(\sin \widehat C = \displaystyle {{AB} \over {BC}} = {{21} \over {35}} = {3 \over 5} = 0,6\)

Loigiaihay.com