Bài 8.1, 8.2, 8.3, 8.4 phần bài tập bổ sung trang 50 SBT toán 7 tập 2

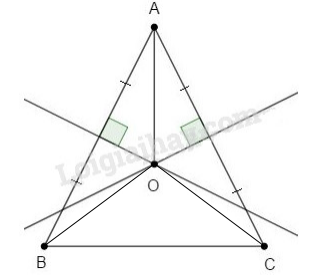
Bài 8.1

Cho tam giác cân (không đều) \(ABC\) có \(AB = AC.\) Hai đường trung trực của hai cạnh \(AB, AC\) cắt nhau tại \(O.\) Khi đó khẳng định nào sau đây là đúng?

\(\left( A \right)OA > OB\)

\(\left( B \right)\widehat {AOB} > \widehat {AOC}\)

\(\left( C \right)AO \bot BC\)

(D) \(O\) cách đều ba cạnh của tam giác \(ABC\)

Phương pháp giải:

Sử dụng: 

+) Ba đường trung trực của tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

+) Điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đường thẳng đó.

+) Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường phân giác ứng với cạnh này.

Lời giải chi tiết:

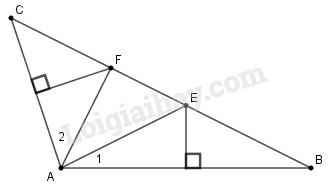
Vì \(O\) thuộc đường trung trực của cạnh \(AB\) nên \(OA = OB.\) 

Vì ba đường trung trực của một tam giác đồng quy nên \(OA\) là đường trung trực của \(BC,\) do đó \(AO \bot BC\).

Vì tam giác \(ABC\) cân tại \(A\) nên đường trung trực \(AO\) đồng thời là đường phân giác của góc \(A,\)

Xét \(∆AOB\) và \( ∆AOC,\) có:

+) \(AB=AC\) (gt)

+) \(\widehat {BAO} = \widehat {CAO}\,\,\) (do \(AO\) là đường phân giác của góc \(A)\)

+) Cạnh \(OA\) chung

Do đó \(∆AOB = ∆AOC (c-g-c),\) suy ra \(\widehat {AOB} = \widehat {AOC}.\)

Từ đó tam giác \(ABC\) cân tại \(A\) nhưng không là tam giác đều nên \(O\) không là giao điểm của ba đường phân giác của tam giác \(ABC.\) Vậy \(O\) không cách đều ba cạnh của tam giác \(ABC.\)

Vậy chỉ có đáp án C đúng.

Chọn \(\left( C \right)AO \bot BC\).

Bài 8.2

Cho tam giác \(ABC\) vuông tại \(A. \) Gọi \(P, Q, R\) lần lượt là trung điểm của ba cạnh \(AB, AC, BC.\) Gọi \(O\) là giao điểm của ba đường phân giác. Khi đó, tâm đường trong ngoại tiếp tam giác \(ABC\) là điểm:

(A) \(O\)                   (B) \(P;\)

(C) \(Q; \)                (D) \(R.\)

Hãy chọn phương án đúng.

Phương pháp giải:

Sử dụng: 

+) Điểm cách đều ba đỉnh của tam giác là tâm đường tròn ngoại tiếp tam giác đó.

+) Sử dụng kết quả bài 66 trang 49 SBT toán 7 tập 2: "Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền"

Lời giải chi tiết:

Vì tam giác \(ABC\) vuông tại \(A\) có \(R\) là trung điểm cạnh huyền \(BC\) nên \(RA = RB = RC = \dfrac{{BC}}{2}\) (theo kết quả bài 66 trang 49 SBT toán 7 tập 2)

Hay \(R\) cách đều ba đỉnh của tam giác \(ABC\) nên \(R\) là tâm đường trong ngoại tiếp tam giác \(ABC.\)

Chọn (D) 

Sử dụng kết quả bài 66 trang 49 SBT toán 7 tập 2

Bài 8.3

Cho tam giác \(ABC\) có \(Â = 100°.\) Các đường trung trực của \(AB\) và \(AC\) lần lượt cắt \(BC\) ở \(E\) và \(F.\) Tính \(\widehat {{\rm{EAF}}}.\)

Phương pháp giải:

Sử dụng: 

+) Tính chất tam giác cân

+) Điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đường thẳng đó.

+) Tổng ba góc trong tam giác bằng \(180^0\) 

Lời giải chi tiết:

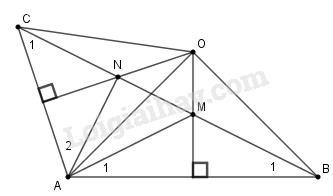
Vì \(E\) thuộc đường trung trực của đoạn thẳng \(AB\) nên \(EA = EB,\) hay tam giác \(EAB\) cân tại đỉnh \(E. \) Suy ra \(\widehat B = \widehat {{A_1}}\)

Vì \(F\) thuộc đường trung trực của đoạn thẳng \(AC\) nên \(FA = FC,\) hay tam giác \(FAC\) cân tại đỉnh \(F. \) Suy ra \(\widehat C = \widehat {{A_2}}\). Ta có: 

\(\widehat {{\rm{EAF}}} = \widehat A - \left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) \)\(= \widehat A - \left( {\widehat B + \widehat C} \right)\)

Mặt khác, xét tam giác \(ABC\) ta có: \(\widehat B + \widehat C+ \widehat A = 180^\circ  \) (tổng ba góc trong tam giác)

Suy ra: \(\widehat B + \widehat C = 180^\circ  - \widehat A \)\(= 180^\circ  - 100^\circ  = 80^\circ \)

Do đó \(\widehat {{\rm{EAF}}} = 100^\circ  - 80^\circ  = 20^\circ \)

Bài 8.4

Cho tam giác \(ABC\) có góc \(A\) là góc tù. Các đường trung trực của \(AB; AC\) cắt nhau tại \(O\) và lần lượt cắt \(BC\) tại \(M, N.\) Chứng minh rằng \(AO\) là tia  phân giác của góc \(MAN.\)

Phương pháp giải:

Sử dụng: 

+) Điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đường thẳng đó.

+) Ba đường trung trực của tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.

Lời giải chi tiết:

Vì \(M\) thuộc đường trung trực của đoạn thẳng \(AB\) nên \(MA = MB,\) hay tam giác \(MAB\) cân tại đỉnh \(M. \) Suy ra \(\widehat {B_1} = \widehat {{A_1}}\) (1)

Vì \(N\) thuộc đường trung trực của đoạn thẳng \(AC\) nên \(NA = NC,\) hay tam giác \(NAC\) cân tại đỉnh \(N. \) Suy ra \(\widehat {C_1} = \widehat {{A_2}}\) (2)

Ta có \(O\) là giao điểm của ba đường trung trực của tam giác \(ABC\) nên \(OA = OB = OC,\) hay các tam giác \(OAB, OAC, OBC\) cân tại \(O.\)

Suy ra, theo tính chất tam giác cân thì \(\widehat {OAB} = \widehat {OBA}\) (*),  \(\widehat {OAC} = \widehat {OC{\rm{A}}}\) (**), \(\widehat {OBC} = \widehat {OCB}\) (4)

Từ (1) và (*) ta có: \(\widehat {MAO} = \widehat {OAB} - \widehat {{A_1}} = \widehat {OBA} - \widehat {{B_1}} = \widehat {OBM}\)

Hay \(\widehat {MAO} = \widehat {OBM}\) (5)

Từ (2) và (**) ta có: \(\widehat {OCN} = \widehat {OCA} - \widehat {{C_1}} \)\(= \widehat {OAC} - \widehat {{A_2}} = \widehat {OAN}\)

Hay \(\widehat {OCN}  = \widehat {OAN}\) (6)

Từ (4), (5) và (6) ta có: \(\widehat {OAM} = \widehat {OBC} = \widehat {OCB} = \widehat {OAN}.\)

Hay \(\widehat {OAM}= \widehat {OAN}\)

Vậy \(OA\) là tia phân giác góc \(MAN.\)

Loigiaihay.com