Bài 65 trang 49 SBT toán 7 tập 2

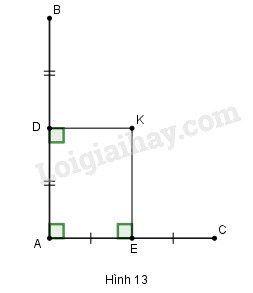
Đề bài

Cho hình 13. Chứng minh rằng ba điểm \(B, K, C\) thẳng hàng. 

Lời giải chi tiết

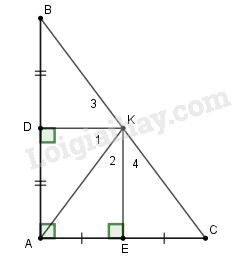
Nối \(KA, KB, KC.\) 

Ta có \(KD\) là đường trung trực của \(AB\)

\( \Rightarrow  KA = KB\) (tính chất đường trung trực)

\( \Rightarrow  ∆KAB\) cân tại \(K\) nên \(KD\) là đường phân giác của \(\widehat {AKB}\)

\( \Rightarrow \) \(\widehat {{K_1}} = \widehat {{K_3}}\)

\( \Rightarrow \) \(\widehat {AKB} = 2\widehat {{K_1}}\)   (1)

Vì \(KE\) là đường trung trực của \(AC\)

\( \Rightarrow  KA = KC\) (tính chất đường trung trực)

\( \Rightarrow  ∆KAC\) cân tại \(K\) nên \(KE\) là đường phân giác của \(\widehat {AKC}\)

\( \Rightarrow \) \(\widehat {{K_2}} = \widehat {{K_4}}\)

\( \Rightarrow \widehat {AKC} = 2\widehat {{K_2}}\left( 2 \right)\)

Ta có:

\(\eqalign{
& K{\rm{D}} \bot AB\left( {gt} \right) \cr 
& AC \bot AB\left( {gt} \right) \cr} \)

Suy ra \(KD // AC\)

Mà \(KE\bot AC\) nên \(KE\bot KD\) hay \(\widehat {DKE} = {90^o}\)

Từ (1) và (2) ta có:

\(\widehat {AKB} + \widehat {AKC} = 2\left( {\widehat {{K_1}} + \widehat {{K_2}}} \right) \)\(\,= 2.\widehat {DKE} = {2.90^o} = {180^o}\)

Do đó \(B, K, C\) thẳng hàng.

Loigiaihay.com