Giải bài 8 trang 32 sách bài tập toán 12 - Chân trời sáng tạoKhảo sát và vẽ đồ thị của các hàm số sau: a) (y = frac{{{x^2} - 2{rm{x}} + 2}}{{{rm{x}} - 1}}); b) (y = - 2{rm{x}} + frac{1}{{2{rm{x}} + 1}}). Quảng cáo
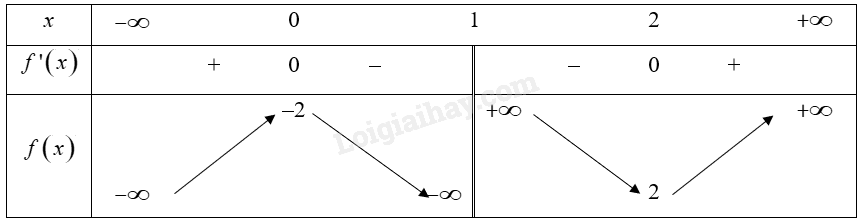
Đề bài Khảo sát và vẽ đồ thị của các hàm số sau: a) \(y = \frac{{{x^2} - 2{\rm{x}} + 2}}{{{\rm{x}} - 1}}\); b) \(y = - 2{\rm{x}} + \frac{1}{{2{\rm{x}} + 1}}\). Phương pháp giải - Xem chi tiết Sơ đồ khảo sát hàm số: Bước 1. Tìm tập xác định của hàm số. Bước 2. Xét sự biến thiên của hàm số ‒ Tìm đạo hàm \(y'\), xét dấu \(y'\), xác định khoảng đơn điệu, cực trị (nếu có) của hàm số. ‒ Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và tìm các đường tiệm cận của đồ thị hàm số (nếu có). ‒ Lập bảng biến thiên của hàm số. Bước 3. Vẽ đồ thị hàm số ‒ Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ (nếu có và dễ tìm),… ‒ Vẽ các đường tiệm cận của đồ thị hàm số (nếu có). ‒ Vẽ đồ thị hàm số. Lời giải chi tiết a) 1. Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\). 2. Sự biến thiên: • Chiều biến thiên: Đạo hàm \(y' = \frac{{{{\left( {{x^2} - 2{\rm{x}} + 2} \right)}^\prime }\left( {{\rm{x}} - 1} \right) - \left( {{x^2} - 2{\rm{x}} + 2} \right){{\left( {{\rm{x}} - 1} \right)}^\prime }}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}} = \frac{{\left( {2{\rm{x}} - 2} \right)\left( {{\rm{x}} - 1} \right) - \left( {{x^2} - 2{\rm{x}} + 2} \right)}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}} = \frac{{{x^2} - 2{\rm{x}}}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\). \(y' = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 2\) Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến trên mỗi khoảng đó. Trên khoảng \(\left( {0;2} \right)\), \(y' < 0\) nên hàm số nghịch biến trên khoảng đó. • Cực trị: Hàm số đạt cực đại tại \(x = 0\) và ${{y}_{CĐ}}=-2$. Hàm số đạt cực tiểu tại \(x = 2\) và \({y_{CT}} = 2\). • Tiệm cận: Ta có: \(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \left( {\frac{{{x^2} - 2{\rm{x}} + 2}}{{{\rm{x}} - 1}}} \right) = - \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( {\frac{{{x^2} - 2{\rm{x}} + 2}}{{{\rm{x}} - 1}}} \right) = + \infty \) Vậy \(x = 1\) là tiệm cận đứng của đồ thị hàm số đã cho. Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 2{\rm{x}} + 2}}{{x\left( {{\rm{x}} - 1} \right)}} = 1\) và \(b = \mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{{x^2} - 2{\rm{x}} + 2}}{{{\rm{x}} - 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - x + 2}}{{x - 1}} = - 1\) Vậy đường thẳng \(y = {\rm{x}} - 1\) là tiệm cận xiên của đồ thị hàm số đã cho. • Bảng biến thiên:
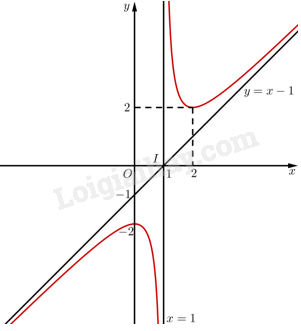
3. Đồ thị Ta có \(y = 0 \Leftrightarrow {x^2} - 2{\rm{x}} + 2 = 0\) (phương trình vô nghiệm). Vậy đồ thị hàm số không có giao điểm với trục \(Ox\). Đồ thị hàm số giao với trục \(Oy\) tại điểm \(\left( {0; - 2} \right)\). Vậy đồ thị hàm số được biểu diễn như hình vẽ.
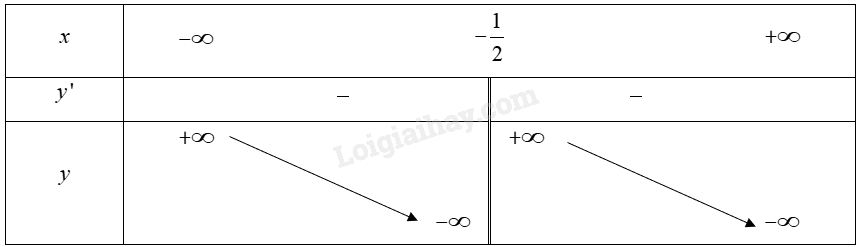
Đồ thị của hàm số có tâm đối xứng là điểm \(I\left( {1;0} \right)\). b) \(y = - 2{\rm{x}} + \frac{1}{{2{\rm{x}} + 1}} = \frac{{ - 4{{\rm{x}}^2} - 2{\rm{x}} + 1}}{{2{\rm{x}} + 1}}\) 1. Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{2}} \right\}\). 2. Sự biến thiên: • Chiều biến thiên: Đạo hàm \(y' = - 2 - \frac{2}{{{{\left( {2{\rm{x}} + 1} \right)}^2}}}\). Vì \(y' < 0\) với mọi \(x \ne - \frac{1}{2}\) nên hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right)\). • Tiệm cận: Ta có: \(\mathop {\lim }\limits_{x \to - {{\frac{1}{2}}^ - }} y = \mathop {\lim }\limits_{x \to - {{\frac{1}{2}}^ - }} \left( {\frac{{ - 4{{\rm{x}}^2} - 2{\rm{x}} + 1}}{{2{\rm{x}} + 1}}} \right) = - \infty ;\mathop {\lim }\limits_{x \to - {{\frac{1}{2}}^ + }} y = \mathop {\lim }\limits_{x \to - {{\frac{1}{2}}^ + }} \left( {\frac{{ - 4{{\rm{x}}^2} - 2{\rm{x}} + 1}}{{2{\rm{x}} + 1}}} \right) = + \infty \) Vậy \(x = - \frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số đã cho. Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 4{{\rm{x}}^2} - 2{\rm{x}} + 1}}{{x\left( {2{\rm{x}} + 1} \right)}} = - 2\) và \(b = \mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) + 2x} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ { - 2{\rm{x}} + \frac{1}{{2{\rm{x}} + 1}} + 2x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{2{\rm{x}} + 1}} = 0\) Vậy đường thẳng \(y = 2{\rm{x}}\) là tiệm cận xiên của đồ thị hàm số đã cho. • Bảng biến thiên:
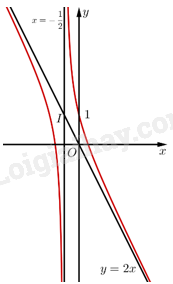
3. Đồ thị Ta có \(y = 0 \Leftrightarrow - 4{{\rm{x}}^2} - 2{\rm{x}} + 1 = 0 \Leftrightarrow x = \frac{{ - 1 + \sqrt 5 }}{4}\) hoặc \(x = \frac{{ - 1 - \sqrt 5 }}{4}\). Vậy đồ thị hàm số giao với trục \(Ox\) tại hai điểm \(\left( {\frac{{ - 1 + \sqrt 5 }}{4};0} \right)\) và \(\left( {\frac{{ - 1 - \sqrt 5 }}{4};0} \right)\). Đồ thị hàm số giao với trục \(Oy\) tại điểm \(\left( {0;1} \right)\). Vậy đồ thị hàm số được biểu diễn như hình vẽ.
Đồ thị của hàm số có tâm đối xứng là điểm \(I\left( { - \frac{1}{2};1} \right)\).
|




















Danh sách bình luận