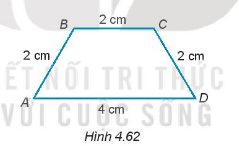
Giải bài 4.60 trang 74 sách bài tập toán 7 - Kết nối tri thức với cuộc sốngCho hình thang cân ABCD có đáy lớn AD đáy nhỏ BC thoả mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD Quảng cáo
Đề bài Cho hình thang cân ABCD có đáy lớn AD đáy nhỏ BC thoả mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.
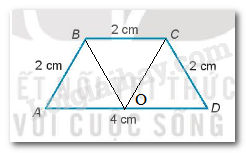
Phương pháp giải - Xem chi tiết - Gọi O là trung điểm của AD. - Chứng minh \(\Delta ABO = \Delta CBO\left( {c - g - c} \right)\) - Chứng minh tam giác OCD đều. Lời giải chi tiết
Gọi O là trung điểm của AD. Khi đó, AO = OD = \(\dfrac{1}{2}.AD= \dfrac{1}{2}.4=2 cm\) Vì vậy \(\widehat {CBO} = \widehat {BOA} = \widehat {OBA}\) Xét \(\Delta ABO\) và \(\Delta CBO\) có: BA = BC (= 2cm) \(\widehat {OBA} = \widehat {OBC}\left( {cmt} \right)\) BO: Cạnh chung Vậy \(\Delta ABO = \Delta CBO\left( {c - g - c} \right)\) Do đó \(OC = OA\) (2 cạnh tương ứng) nên OA = OC = OD = 2 cm Vậy tam giác OCD là tam giác đều. Như vậy \(\widehat A = \widehat D = {60^0}\) Vì ABCD là hình thang có 2 đáy là BC và AD nên BC // AD nên \(\widehat B + \widehat A = 180^0;\widehat C + \widehat D = 180^0 \) (2 góc trong cùng phía) Do đó, \(\widehat B = \widehat C = {180^0} - {60^0} = {120^0}.\)
|




















Danh sách bình luận