Bài 46 trang 141 Vở bài tập toán 7 tập 1

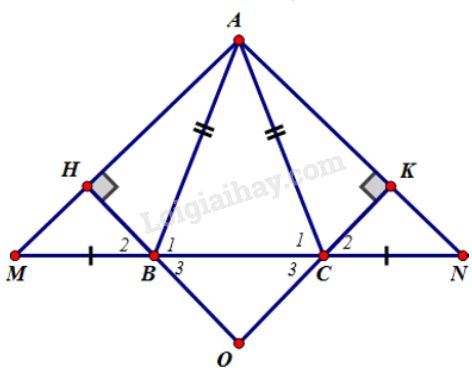
Đề bài

Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của \(BC\) lấy điểm \(M\), trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(BM = CN.\)

a) Chứng minh rằng tam giác \(AMN\) là tam giác cân.

b) Kẻ \(BH ⊥ AM\) (\(H \in AM\)), kẻ \(CK ⊥ AN\; (K  \in  AN).\) Chứng minh rằng \(BH = CK.\)

c) Chứng minh rằng \(AH = AK.\)

d) Gọi \(O\) là giao điểm của \(HB\) và \(KC.\) Tam giác \(OBC\) là tam giác gì? Vì sao?

e) Khi \(\widehat {BAC} = {60^o}\) và \(BM = CN = BC,\) hãy tính số đo các góc của tam giác \(AMN\) và xác định dạng của tam giác \(OBC.\)

Lời giải chi tiết

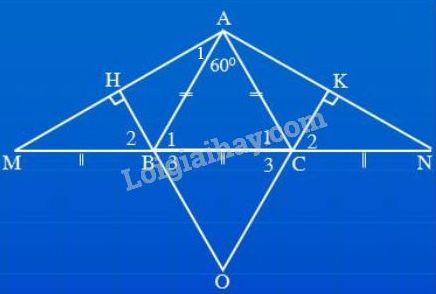
a) \(∆ABC\) cân tại \(A\), \( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\) (góc đáy của tam giác cân).

\(\Rightarrow \widehat {ABM} = \widehat {ACN}\) (cùng bù với hai góc bằng nhau \( \widehat {{B_1}} = \widehat {{C_1}}\))

\(∆ABM \) và \(∆ACN \) có:

\(AB = AC\) (vì \(∆ABC\) cân tại \(A\))

\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên)

\(BM = CN\) (gt)

Do đó \( ∆ABM = ∆ACN\) (c.g.c)

suy ra \( \widehat M = \widehat N\) (hai góc tương ứng)

Tam giác \(AMN\) có \( \widehat M = \widehat N\) nên là tam giác cân.

b) Các tam giác vuông \(BHM\) và \(CKN\) có :

cạnh huyền \(BM = CN\) (gt)

góc nhọn \(\widehat M = \widehat N\) (chứng minh trên)

Do đó \( ∆BHM  = ∆CKN\) (cạnh huyền - góc nhọn)

suy ra \( BH = CK\) (hai cạnh tương ứng)

c) Các tam giác vuông \(ABH\) và \(ACK\) có:

cạnh huyền \(AB=AC\) (vì \(∆ABC\) cân tại \(A\))

cạnh góc vuông \( BH = CK\) (chứng minh câu b)

Do đó \(\Delta ABH=\Delta ACK\)

suy ra \(AH = AK\) (hai cạnh tương ứng).

d) \(∆BHM = ∆CKN\) (câu b)

suy ra \(\widehat {{B_2}} = \widehat {{C_2}}\) (hai góc tương ứng)

Ta lại có \(  \widehat {{B_3}}=\widehat {{B_2}} \) (đối đỉnh); \(  \widehat {{C_3}}=\widehat {{C_2}}\) (đối đỉnh) nên \(\widehat {{B_3}} = \widehat {{C_3}}\).

Tam giác \(OBC\) có \(\widehat {{B_3}} = \widehat {{C_3}}\) nên là tam giác cân tại \(O.\)

e) (h75) Ta có thêm \(\widehat {BAC} = {60^o}\) và \(BM = CN = BC\).

\(\Delta ABC\) cân có \(\widehat {A} = {60^o}\) nên là tam giác đều suy ra \(\widehat {{B_1}} = \widehat {{C_1}} = \widehat {BAC} = {60^o}\).

Tam giác \(ABM\) có \(AB=BM\) (cùng bằng \(BC\)) nên là tam giác cân, suy ra \(\widehat M = \widehat {BAM}\)

Ta lại có \(\widehat M + \widehat {{A_1}} = \widehat {{B_1}} = {60^o}\) nên \(\widehat M = \widehat {{A_1}} = {60^o}:2 = {30^o}\)

Chứng minh tương tự, ta được: \(\widehat N = {30^o}\)

Tam giác \(AMN\) có \(\widehat M = \widehat N = {30^o}\) nên \(\widehat {MAN} = {180^o} - {30^o} - {30^o} = {120^o}\)

Tam giác \(BHM\) vuông tại \(H\) có \(\widehat M = {30^o}\) nên \(\widehat {{B_2}} = {90^o} - {30^o} = {60^o}\)

\(\widehat {{B_3}} = \widehat {{B_2}} = {60^o}\)

Tam giác \(OBC\) cân (câu d) có \(\widehat {{B_3}} = {60^o}\) nên tam giác \(OBC\) là tam giác đều.

Loigiaihay.com