Bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 177 SBT toán 9 tập 2Giải bài 4.4, 4.5, 4.6 phần bài tập bổ sung trang 177 sách bài tập toán 9. Thể tích và diện tích của hình cầu thay đổi thế nào nếu bán kính hình cầu: a) Tăng gấp 2 lần? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
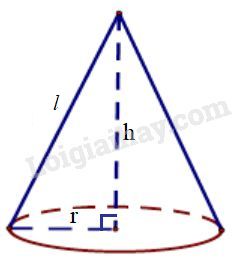
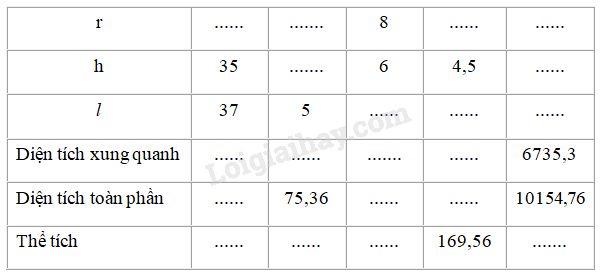
Bài IV.4 Thể tích và diện tích của hình cầu thay đổi thế nào nếu bán kính hình cầu: a) Tăng gấp \(2\) lần? b) Tăng gấp \(3\) lần? c) Giảm đi \(2\) lần? Phương pháp giải: Sử dụng: - Diện tích mặt cầu bán kính \(r\) là: \(S = 4\pi {r^2}\). - Thể tích hình cầu bán kính \(r\) là: \(\displaystyle V ={4 \over 3}\pi {r^3}\). Lời giải chi tiết: Hình cầu có bán kính \(R\) có thể tích là: \(\displaystyle V = {4 \over 3}\pi {R^3}\) và diện tích \(S = 4\pi {R^2}\). a) Nếu tăng bán kính gấp \(2\) lần thì Thể tích hình cầu là: \(\displaystyle{V_1} = {4 \over 3}\pi {\left( {2R} \right)^3} = 8.{4 \over 3}\pi {R^3} = 8V\) Diện tích hình cầu là: \({S_1} = 4\pi {\left( {2R} \right)^2} = 4.4\pi {R^2} = 4S\) b) Nếu tăng bán kính gấp \(3\) lần thì Thể tích hình cầu là: \(\displaystyle {V_2} = {4 \over 3}\pi {\left( {3R} \right)^3} = 27.{4 \over 3}\pi {R^3} = 27V\) Diện tích hình cầu là: \({S_2} = 4\pi {\left( {3R} \right)^2} = 9.4\pi {R^2} = 9S\) c) Nếu giảm bán kính đi \(2\) lần thì Thể tích hình cầu là: \(\displaystyle {V_3} = {4 \over 3}\pi {\left( {{R \over 2}} \right)^3} = {1 \over 8}.{4 \over 3}\pi {R^3} = {1 \over 8}V\) Diện tích hình cầu là: \(\displaystyle {S_3} = 4\pi {\left( {{R \over 2}} \right)^2} = {1 \over 4}.4\pi {R^2} = {1 \over 4}S\). Bài IV.5 Quan sát hình nón ở hình bs.31 rồi điền số thích hợp và các ô trống trong bảng sau (lấy \(\pi = 3,14)\))
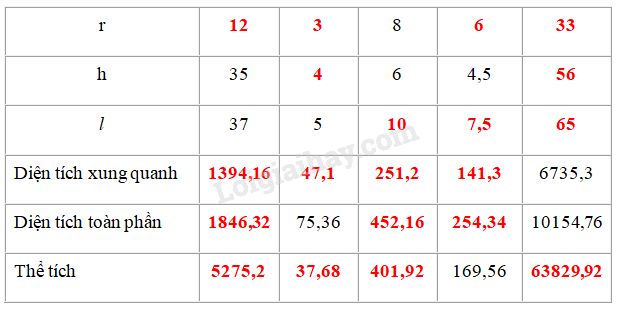
Phương pháp giải: Sử dụng: - Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\). - Diện tích toàn phần của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}\). - Thể tích hình nón: \(\displaystyle V = {1 \over 3}\pi {r^2}h\). (\(r\) là bán kính đường tròn đáy, \( l\) là đường sinh, \(h\) là chiều cao). Lời giải chi tiết: Ta điền được bảng sau:
Giải thích: * Hình nón có \(h=35;l=37\) Áp dụng định lí Pytago ta có: \(r = \sqrt {{l^2} - {h^2}} = \sqrt {{{37}^2} - {{35}^2}} = 12\) \({S_{xq}} = \pi rl = 3,14.12.37 = 1394,16\) \({S_{TP}} = {S_{xq}} + \pi {r^2} \)\(\,= 1394,16 + 3,{14.12^2} = 1846,32\) \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.3,{14.12^2}.35 \)\(\,= 5275,2\) * Hình nón có \(l=5; S_{TP}=75,36\) \(\begin{array}{l} \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{5^2} - {3^2}} = 4\) \({S_{xq}} = \pi rl = 3,14.3.5 = 47,1\) \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.3,{14.3^2}.4 = 37,68\) * Hình nón có \(r=8;h=6\) \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{8^2} + {6^2}} = 10\) \({S_{xq}} = \pi rl = 3,14.8.10 = 251,2\) \({S_{TP}} = \pi rl + \pi {r^2} = 251,2 + 3,{14.8^2}\)\(\, = 452,16\) \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.3,{14.8^2}.6 = 401,92\) * Hình nón có \(h=4,5, V=169,56\) \(V = \dfrac{1}{3}\pi {r^2}h \) \(\Rightarrow r = \sqrt {\dfrac{{3V}}{{\pi h}}} = \sqrt {\dfrac{{3.169,56}}{{3,14.4,5}}} = 6\) \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{6^2} + 4,{5^2}} = 7,5\) \({S_{xq}} = \pi rl = 3,14.6.7,5 = 141,3\) \({S_{TP}} = \pi rl + \pi {r^2} = 141,3 + 3,{14.6^2}\)\(\, = 254,34\) * Hình nón có \(S_{xq}=6735,3;\;S_{TP}=10154,76\) \(\begin{array}{l} \({S_{xq}} = \pi rl \) \(\Rightarrow l = \dfrac{{{S_{xq}}}}{{\pi r}} = \dfrac{{6735,3}}{{3,14.33}} = 65\) \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{65}^2} - {{33}^2}} = 56\) \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.3,{14.33^2}.56 \)\(\,= 63829,92\) Bài IV.6 Quan sát hình cầu ở hình bs.32 rồi điền số thích hợp vào các ô trống trong bảng sau (lấy \(\pi = 3,14)\))
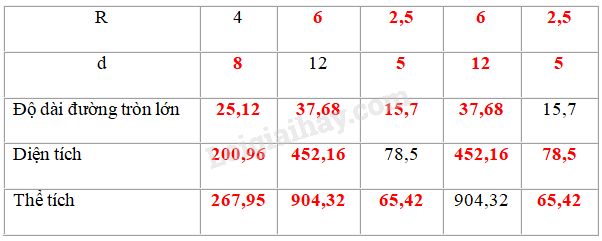
Phương pháp giải: Sử dụng: - Diện tích mặt cầu bán kính \(r\) là: \(S = 4\pi {r^2}\). - Thể tích hình cầu bán kính \(r\) là: \(\displaystyle V ={4 \over 3}\pi {r^3}\). Lời giải chi tiết: Ta điền được bảng sau:
Giải thích: * Hình cầu có \(R=4\) \(d=2R=2.4=8\) Độ dài đường tròn lớn là: \(C = 2\pi R = 2.3,14.4 = 25,12\) \(S = 4\pi {R^2} = 4.3,{14.4^2} = 200,96\) \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}.3,{14.4^3} \approx 267,95\) * Hình cầu có \(d=12\) \(\begin{array}{l} * Hình cầu có \(S=78,5\) \(S = 4\pi {R^2} \Rightarrow R = \sqrt {\dfrac{S}{{4\pi }}} = \sqrt {\dfrac{{78,5}}{{4.3,14}}} \)\(\, = 2,5\) \(d = 2R = 2.2,5 = 5\) \(C = 2\pi R = 2.3,14.2,5 = 15,7\) \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}.3,14.2,{5^3} \approx 65,42\) * Hình cầu có \(V=904,32\) \(V = \dfrac{4}{3}\pi {R^3} \Rightarrow R = \sqrt[3]{{\dfrac{{3V}}{{4\pi }}}}\)\(\, = \sqrt[3]{{\dfrac{{3.904,32}}{{4.3,14}}}} = 6\) \(d = 2R = 2.6 = 12\) \(C = 2\pi R = 2.3,14.6 = 37,68\) \(S = 4\pi {R^2} = 4.3,{14.6^2} = 452,16\) * Hình cầu có \(C=15,7\) \(C = 2\pi R \) \(\Rightarrow R = \dfrac{C}{{2\pi }} = \dfrac{{15,7}}{{2.3,14}} = 2,5\) \(d = 2R = 2.2,5 = 5\) \(S = 4\pi {R^2} = 4.3,14.2,{5^2} = 78,5\) \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}.3,14.2,{5^3} \approx 65,42\) Loigiaihay.com
|





















Danh sách bình luận