Bài 4.1, 4.2, 4.3 phần bài tập bổ sung trang 14 SBT toán 7 tập 1

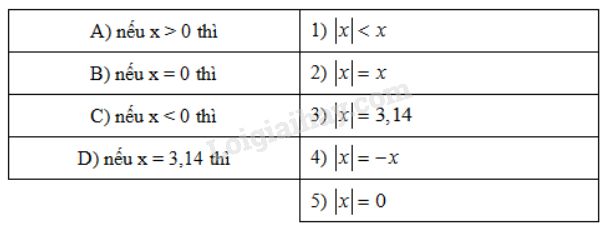
Bài 4.1

Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng:

Với \(x\) là số hữu tỉ:

Phương pháp giải:

Giá trị tuyệt đối của một số hữu tỉ \(x\), kí hiệu là \(|x|\), là khoảng cách từ điểm \(x\) tới điểm \(0\) trên trục số. 

Nhận xét: Giá trị tuyệt đối của số hữu tỉ luôn luôn không âm.

\(\left | x \right |=\left\{\begin{matrix} x& \text{nếu} & x \geq 0 \\ -x& \text{nếu} & x < 0 \end{matrix}\right.\)

Lời giải chi tiết:

A) - 2); B) - 5); C) - 4); D) - 3) 

(Lưu ý: B có thể nối với 2) hoặc với 4).

Bài 4.2

Cho \(A = -12,7 . 32,6 + 2,7 . 12,8 + 12,7 . 2,6 + 2,7 . 17,2\). Giá trị của biểu thức \(A\) là:

(A) \(- 300\);                       (B) \(-200\);

(C) \(300\);                          (D) \(200.\)

Hãy chọn đáp án đúng. 

Phương pháp giải:

Áp dụng tính chất phân phối giữa phép nhân và phép cộng:

\(ab+ac=a(b+c)\)

Lời giải chi tiết:

\(\begin{array}{l}
A = - 12,7.32,6 + 2,7.12,8 + 12,7.2,6 + 2,7.17,2\\
= \left( {12,7.2,6 - 12,7.32,6} \right) + \left( {2,7.12,8 + 2,7.17,2} \right)\\
= 12,7.\left( {2,6 - 32,6} \right) + 2,7.\left( {12,8 + 17,2} \right)\\
= 12,7.\left( { - 30} \right) + 2,7.30\\
= 30.\left( { - 12,7} \right) + 30.2,7\\
= 30.\left( { - 12,7 + 2,7} \right)\\
= 30.\left( { - 10} \right) = - 300
\end{array}\)

Chọn (A). 

Bài 4.3

Cho \(a = -6, b = 3, c = -2\).

Tính: \(\left| {a + b - c} \right|;\left| {a - b + c} \right|;\left| {a - b - c} \right|\) 

Phương pháp giải:

Giá trị tuyệt đối của một số hữu tỉ \(x\), kí hiệu là \(|x|\), là khoảng cách từ điểm \(x\) tới điểm \(0\) trên trục số. 

Nhận xét: Giá trị tuyệt đối của số hữu tỉ luôn luôn không âm.

\(\left | x \right |=\left\{\begin{matrix} x& \text{nếu} & x \geq 0 \\ -x& \text{nếu} & x < 0 \end{matrix}\right.\)

Lời giải chi tiết:

\(\left| {a + b - c} \right| = \left| { - 6 + 3 - ( - 2)} \right| \)

\(= \left| { - 6 + 3 + 2} \right|= \left| { - 1} \right| = 1\)

\(\left| {a - b + c} \right| = \left| { - 6 - 3 + ( - 2)} \right|\)

\(= \left| { - 6 - 3 - 2} \right| = \left| { - 11} \right| = 11\)

\(\left| {a - b - c} \right| = \left| { - 6 - 3 - ( - 2)} \right| \) 

\(= \left| { - 6 - 3 + 2} \right| = \left| { - 7} \right| = 7.\)

 Loigiaihay.com