Bài 4.1, 4.2, 4.3, 4.4 phần bài tập bổ sung trang 143, 144 SBT toán 7 tập 1Giải bài 4.1, 4.2, 4.3, 4.4 phần bài tập bổ sung trang 143, 144 sách bài tập toán 7 tập 1. Bổ sung thêm điều kiện sau thì tam giác ACD = tam giác DBA theo trường hợp cạnh - cạnh – cạnh hoặc cạnh – góc - cạnh. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
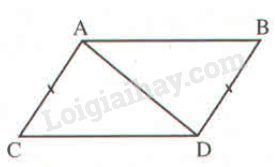
Bài 4.1 Bổ sung thêm điều kiện sau thì \(ΔACD = ΔDBA\) theo trường hợp cạnh - cạnh – cạnh hoặc cạnh – góc - cạnh.
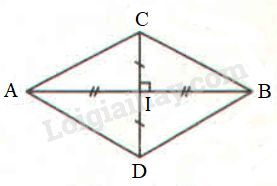
\(\begin{array}{l} Phương pháp giải: - Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. - Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. Lời giải chi tiết: Xét \(ΔACD \) và \( ΔDBA\) có: \(AD\) cạnh chung \(AC=DB\) (gt) a) Thêm điều kiện \(\widehat {ADC} = \widehat {DAB}\) thì ta không thể kết luận \(ΔACD = ΔDBA\). Vì \(\widehat {ADC}\) không xen giữa hai cạnh \(AD\) và \(AC\). b) Thêm điều kiện \(\widehat {ACD} = \widehat {DBA}\) thì ta không thể kết luận \(ΔACD = ΔDBA\). Vì \(\widehat {ACD}\) không xen giữa hai cạnh \(AD\) và \(AC\). c) Thêm điều kiện \(\widehat {CAD} = \widehat {BDA}\) ta kết luận \(ΔACD = ΔDBA\) (c.g.c). d) Thêm điều kiện \(CD=BA\) ta kết luận \(ΔACD = ΔDBA\) (c.c.c). Bài 4.2 Cho hai đoạn thẳng \(AB\) và \(CD\) vuông góc với nhau tại trung điểm của mỗi đoạn. Kẻ các đoạn thẳng \(AC, CB, BD, DA.\) Tìm các tia phân giác của các góc (khác góc bẹt) trên hình. Phương pháp giải: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Lời giải chi tiết:
+ Gọi giao điểm của AB và CD là I. Theo giả thiết I là trung điểm của CD và AB. * Xét \(\Delta ACI \) và \( \Delta BCI\) có: \(AI=BI\) (\(I\) là trung điểm của \(AB\)) \(CI\) chung \(\widehat {AIC} = \widehat {BIC}=90^o\) \( \Rightarrow \Delta ACI = \Delta BCI\) (c.g.c) \( \Rightarrow \widehat {ACI} = \widehat {BCI}\) (hai góc tương ứng) Vậy \(CD\) là tia phân giác của \(\widehat {ACB}\). * Xét \(\Delta ADI \) và \( \Delta BDI\) có: \(AI=BI\) (\(I\) là trung điểm của \(AB\)) \(DI\) chung \(\widehat {AID} = \widehat {BID}=90^o\) \( \Rightarrow \Delta ADI = \Delta BDI\) (c.g.c) \( \Rightarrow \widehat {ADI} = \widehat {BDI}\) (hai góc tương ứng) Vậy \(DC\) là tia phân giác của \(\widehat {ADB}\). *Xét \(\Delta ACI \) và \( \Delta ADI\) \(AI\) chung \(CI=DI\) (\(I\) là trung điểm của \(CD\)) \(\widehat {AIC} = \widehat {AID}=90^o\) \( \Rightarrow \Delta ACI = \Delta ADI\) (c.g.c) \( \Rightarrow \widehat {CAI} = \widehat {DAI}\) (hai góc tương ứng). Vậy \(AB\) là tia phân giác của \(\widehat {CAD}\). *Xét \(\Delta BCI \) và \( \Delta BDI\) \(BI\) chung \(CI=DI\) (\(I\) là trung điểm của \(CD\)) \(\widehat {BIC} = \widehat {BID}=90^o\) \( \Rightarrow \Delta BCI = \Delta BDI\) (c.g.c) \( \Rightarrow \widehat {CBI} = \widehat {DBI}\) (hai góc tương ứng). Vậy \(BA\) là tia phân giác của \(\widehat {CBD}\). Bài 4.3 Cho tam giác nhọn \(ABC\), \(M\) là trung điểm của \(BC.\) Đường vuông góc với \(AB\) tại \(B\) cắt đường thẳng \(AM\) tại \(D.\) Trên tia \(MA\) lấy điểm \(E\) sao cho \(ME = MD.\) Chứng minh rằng \(CE\) vuông góc với \(AB\). Phương pháp giải: - Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. - Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại. Lời giải chi tiết:
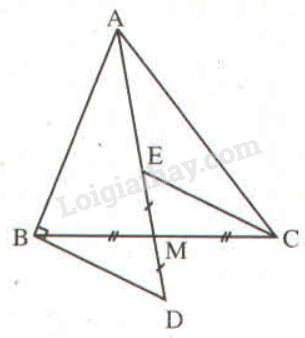
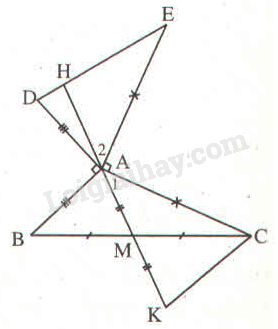
Xét \(ΔBMD\) và \(ΔCME\) có: \(BM = MC\) (vì M là trung điểm BC) \(\widehat {BMD} = \widehat {CME}\) (hai góc đối đỉnh) \(ME = MD\) (giả thiết) \(⇒ ΔBMD = ΔCME\) (c.g.c) \(⇒ \widehat D = \widehat {MEC}\) (hai góc tương ứng) Mà \(\widehat D \) và \( \widehat {MEC}\) ở vị trí so le trong nên \(BD // CE.\) Ta có \(AB ⊥\, BD, BD // CE\) nên \(AB ⊥ CE.\) Bài 4.4 Cho tam giác \(ABC\) có \(\widehat A = {110^o}\), \(M\) là trung điểm của \(BC.\) Trên tia đối của tia \(MA\) lấy điểm \(K\) sao cho \(MK = MA.\) a) Tính số đo của góc \(ACK.\) b) Vẽ về phía ngoài của tam giác \(ABC\) các đoạn thẳng \(AD, AE\) sao cho \(AD\) vuông góc với \(AB\) và \(AD = AB, AE\) vuông góc với \(AC\) và \(AE = AC.\) Chứng minh rằng \(ΔCAK = ΔAED\). c) Chứng minh rằng \(MA\) vuông góc với \(DE.\) Phương pháp giải: - Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. - Tổng các góc của một tam giác bằng \(180^o\). Lời giải chi tiết:
a) Xét \(ΔAMB\) và \(ΔKMC\) có: \(AM = MK\) (gt) \(BM = MC\) (vì \(M\) là trung điểm của \(BC\)) \(\widehat {AMB} = \widehat {KMC}\) (hai góc đối đỉnh) \(⇒ ΔAMB = ΔKMC\) (c.g.c) \(⇒ \widehat {BAM} = \widehat {CKM}\) (hai góc tương ứng). Mà \(\widehat {BAM} \) và \( \widehat {CKM}\) ở vị trí so le trong nên \( CK // AB\). \(\widehat {ACK} + \widehat {BAC} = {180^o}\) (hai góc trong cùng phía) \(\begin{array}{l} b) Ta có: \(\widehat {DAE} + \widehat {DAB} + \widehat {BAC} + \widehat {CAE} \)\(\,= {360^o}\) Mà \(\widehat {DAB} = \widehat {CAE} = {90^o};\widehat {BAC} = {110^o}\) \(\widehat {DAE} = {360^o} - {90^o} - {90^o} - {110^o}\)\(\, = {70^o}\) \(⇒ \widehat {DAE} = \widehat {KCA}\). Xét \(ΔCAK\) và \(ΔAED\) có: \(AC = AE\) (gt) \( \widehat {KCA}=\widehat {DAE} \) (chứng minh trên) \(CK = AD\) (cùng bằng \(AB\)) \(⇒ ΔCAK = ΔAED\) (c.g.c) c) Gọi \(H\) là giao điểm của \(MA\) và \(DE.\) \(ΔCAK = ΔAED\) (câu b) suy ra \(\widehat {{A_1}} = \widehat E\) (hai góc tương ứng). Ta lại có \(\widehat {{A_1}} +\widehat {CAE}+ \widehat {{A_2}} = {90^o}\) \( \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} \)\(=180^0-\widehat {CAE}=180^0-90^0\) \(\Rightarrow \widehat {{A_1}} + \widehat {{A_2}} = {90^o}\) \( \Rightarrow \widehat {{A_2}} + \widehat E = {90^o}\) Áp dụng định lí tổng các góc của một tam giác vào \(\Delta AHE\), ta có: \(\begin{array}{l} Vậy \(MA ⊥ DE.\) Loigiaihay.com
|















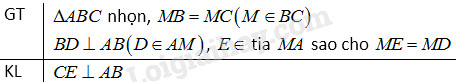







Danh sách bình luận