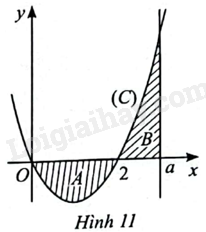
Giải bài 4 trang 21 sách bài tập toán 12 - Chân trời sáng tạoCho hàm số (y = {x^2} - 2x) có đồ thị (left( C right)). Kí hiệu (A) là hình phẳng giới hạn bởi (left( C right)), trục hoành và hai đường thẳng (x = 0,x = 2); (B) là hình phẳng giới hạn bởi (left( C right)), trục hoành và hai đường thẳng (x = 2,x = aleft( {a > 2} right)). Tìm giá trị của (a) để (A) và (B) có diện tích bằng nhau. Quảng cáo
Đề bài Cho hàm số \(y = {x^2} - 2x\) có đồ thị \(\left( C \right)\). Kí hiệu \(A\) là hình phẳng giới hạn bởi \(\left( C \right)\), trục hoành và hai đường thẳng \(x = 0,x = 2\); \(B\) là hình phẳng giới hạn bởi \(\left( C \right)\), trục hoành và hai đường thẳng \(x = 2,x = a\left( {a > 2} \right)\). Tìm giá trị của \(a\) để \(A\) và \(B\) có diện tích bằng nhau.
Phương pháp giải - Xem chi tiết Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \). Lời giải chi tiết Ta có: \(\begin{array}{l}{S_A} = \int\limits_0^2 {\left| {{x^2} - 2{\rm{x}}} \right|dx} = \int\limits_0^2 {\left( { - {x^2} + 2{\rm{x}}} \right)dx} = \left. {\left( { - \frac{{{x^3}}}{3} + {x^2}} \right)} \right|_0^2 = \frac{4}{3}\\{S_B} = \int\limits_2^a {\left| {{x^2} - 2{\rm{x}}} \right|dx} = \int\limits_2^a {\left( {{x^2} - 2{\rm{x}}} \right)dx} = \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|_2^a = \frac{{{a^3}}}{3} - {a^2} + \frac{4}{3}\end{array}\) Vì \(A\) và \(B\) có diện tích bằng nhau nên ta có: \(\frac{4}{3} = \frac{{{a^3}}}{3} - {a^2} + \frac{4}{3} \Leftrightarrow \frac{{{a^3}}}{3} - {a^2} = 0 \Leftrightarrow a = 0\) (loại) hoặc \({\rm{a}} = 3\). Vậy với \({\rm{a}} = 3\) thì \(A\) và \(B\) có diện tích bằng nhau.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
