Bài 32 trang 82 Vở bài tập toán 7 tập 2

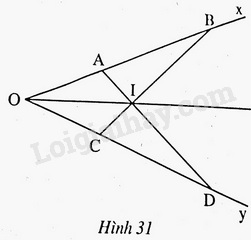
Đề bài

Cho góc \(xOy\) khác góc bẹt. Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\), trên tia \(Oy\) lấy hai điểm \(C\) và \(D\) sao cho \(OA = OC, OB = OD.\) Gọi \(I\) là giao điểm của hai đoạn thẳng \(AD\) và \(BC.\) Chứng minh rằng:

a) \(BC = AD\)

b) \(IA = IC, IB = ID\)

c) Tia \(OI\) là tia phân giác của góc \(xOy\).

Lời giải chi tiết

a) Xét hai tam giác \(OAD\) và \(OCB\). 

Ta có \(OA = OC\) (gt); \(OD = OB\) (gt), góc \(O\) chung

Vậy \(∆AOD =  ∆COB\) (c.g.c)

suy ra \(AD = BC\) (hai cạnh tương ứng).

b) Xét hai tam giác \(AIB\) và \(CID\). Ta có (theo gt)

\(AB = OB - OA = OD - OC = CD.\)

Mặt khác, do \(∆AOD =  ∆COB\) (câu a) suy ra \(\widehat{ABI} = \widehat{CDI}\) và \(\widehat{OAI} = \widehat{OCI}\). Từ \(\widehat{OAI} = \widehat{OCI}\) suy ra \(\widehat{BAI} = \widehat{DCI}\) (cặp góc kề bù với các góc bằng nhau)

Vậy \(∆AIB = ∆CID\) (g.c.g) suy ra \( IC = IA\) và \(ID = IB\) (hai cạnh tương ứng)

c) Ta có \( ∆OBI =  ∆ODI\) (c.c.c), suy ra \(\widehat{AOI} = \widehat{COI}\).

Hơn nữa, hiển nhiên \(I\) nằm bên trong góc \(xOy\). Vậy \(OI\) là tia là phân giác của \(\widehat{xOy}\).

Loigiaihay.com