Giải bài 3 trang 71 SGK Toán 8 – Chân trời sáng tạoCho tam giác nhọn Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Quảng cáo
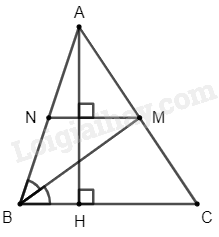
Đề bài Cho tam giác nhọn \(ABC\) có \(AH\) là đường cao. Tia phân giác của góc \(B\) cắt \(AC\) tại \(M\). Từ \(M\) kẻ đường thẳng vuông góc với \(AH\) và cắt \(AB\) tại \(N\). Chứng minh rằng: a) Tứ giác \(BCMN\) là hình thang b) \(BN = MN\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Chứng minh \(NM\) // \(BC\) rồi chỉ ra \(BNMC\) là hình thang b) Chứng minh \(\Delta BNM\) cân tại \(N\) Lời giải chi tiết
a) Ta có: \(NM \bot AH\) (gt) \(BC \bot AH\) (gt) Suy ra \(NM\) // \(BC\) Suy ra \(BNMC\) là hình thang b) Vì \(NM\) // \(BC\) (cmt) Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong) Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác) Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\) Suy ra \(\Delta MNB\) cân tại \(N\) Suy ra \(BN = NM\)
|




















Danh sách bình luận