Bài 29 trang 55 SBT toán 9 tập 2Giải bài 29 trang 55 sách bài tập toán 9. Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
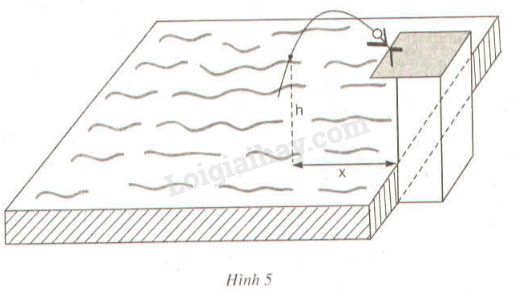
Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách \(x\) từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức: \(h = - {\left( {x - 1} \right)^2} + 4\) Hỏi khoảng cách x bằng bao nhiêu:
LG a Khi vận động viên ở độ cao \(3m\)? Phương pháp giải: Thay \(h=3m\) vào phương trình \(h = - {\left( {x - 1} \right)^2} + 4\), từ đó ta tìm \(x\). Lời giải chi tiết: Khi \(h = 3m\) ta có: \(\eqalign{ Vậy \(x = 0\, m\) hoặc \(x = 2\,m\). LG b Khi vận động viên chạm mặt nước? Phương pháp giải: Khi chạm mặt nước ta có \(h=0\), thay \(h=0\) vào phương trình \(h = - {\left( {x - 1} \right)^2} + 4\) từ đó ta tìm \(x\). * Phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) và \(b = 2b'\), \(\Delta ' = b{'^2} - ac\) + Nếu \(\Delta ' >0\) thì phương trình có hai nghiệm phân biệt: \({x_1}=\dfrac{-b' + \sqrt{\bigtriangleup '}}{a}\); \({x_2}=\dfrac{-b' - \sqrt{\bigtriangleup '}}{a}\) + Nếu \(\Delta ' =0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b'}{a}\). + Nếu \(\Delta ' <0\) thì phương trình vô nghiệm. Lời giải chi tiết: Khi vận động viên chạm mặt nước ta có \(h = 0\). \(\eqalign{ Vì khoảng cách không âm nên \(x = 3\,m\). Loigiaihay.com
|




















Danh sách bình luận