Bài 20 trang 105 SBT toán 7 tập 1

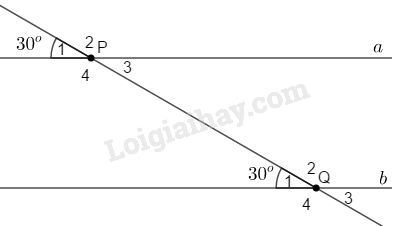
Đề bài

Trên hình 5 người ta cho biết \(a // b\)  và \(\widehat {{P_1}} = \widehat {{Q_1}} = 30^\circ \)

a) Viết tên một cặp góc đồng vị khác và nói rõ số đo mỗi góc.

b) Viết tên một cặp góc so le trong và nói rõ số đo mỗi góc.

c) Viết tên một cặp góc trong cùng phía và nói rõ số đo mỗi góc.

d) Viết tên mỗi cặp góc ngoài cùng phía và cho biết tổng số đo hai góc đó.

Lời giải chi tiết

a) \(\widehat {{P_1}} = \widehat {{P_3}}=30^0\) (hai góc đối đỉnh)

    \(\widehat {{Q_1}} = \widehat {{Q_3}}=30^0\) (hai góc đối đỉnh)

Cặp góc đồng vị khác là: \(\widehat {{P_3}} \) và \( \widehat {{Q_3}} \); \(\widehat {{P_3}} = \widehat {{Q_3}} = 30^\circ \)

b) Cặp góc so le trong là: \(\widehat {{P_3}} \) và \( \widehat {{Q_1}}\);

\(\widehat {{P_3}} = \widehat {{Q_1}} = 30^\circ \)

c) \(\widehat {{P_3}}\) và \(\widehat {{Q_2}}\) là hai góc trong cùng phía.

\(\widehat {{P_3}} = 30^\circ \), ta tính \(\widehat {{Q_2}}\)

\(\widehat {{Q_1}} + \widehat {{Q_2}} = {180^o}\) (hai góc kề bù)

\(\Rightarrow \widehat {{Q_2}} = {180^o} - \widehat {{Q_1}} \)\(\,= {180^o} - {30^o} = {150^o}\)

Vậy: \(\widehat {{P_3}} = 30^\circ ;\widehat {{Q_2}} = 150^\circ \)

d) \(\widehat {{P_1}}\) và \(\widehat {{Q_4}}\) là hai góc ngoài cùng phía. Ta tìm tổng số đo hai góc này.

Ta có: 

\(\widehat {{P_1}} = \widehat {{P_3}}\) (hai góc đối đỉnh)

\(\widehat {{P_3}} = \widehat {{Q_1}} \) (câu b)

\(\Rightarrow \widehat {{P_1}} = \widehat {{Q_1}}\)

\(\widehat {{Q_1}} + \widehat {{Q_4}} = {180^o} \) (hai góc kề bù)

\(\Rightarrow \widehat {{P_1}} + \widehat {{Q_4}} = {180^o}\).

Vậy \(\widehat {{P_1}}\) và \(\widehat {{Q_4}}\) là hai góc ngoài cùng phía và \(\widehat {{P_1}} + \widehat {{Q_4}} = 180^\circ \).

Loigiaihay.com