Bài 20 trang 102 SBT toán 9 tập 2

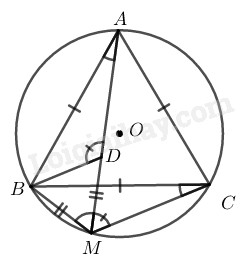
Đề bài

Cho tam giác đều \(ABC\) nội tiếp đường tròn \((O)\) và \(M\) là một điểm của cung nhỏ \(BC.\) Trên \(MA\) lấy điểm \(D\) sao cho \(MD = MB.\)

\(a)\) Hỏi tam giác MBD là tam giác gì\(?\)

\(b)\) So sánh hai tam giác \(BDA\) và \(BMC.\)

\(c)\) Chứng minh rằng \(MA = MB + MC.\)

Lời giải chi tiết

\(a)\) \(MB = MD \;\;(gt)\) \( \Rightarrow \) \(∆MBD\) cân tại \(M\)

\(\widehat {AMB} = \widehat {ACB}\) (\(2\) góc nội tiếp cùng chắn cung \(\overparen{AB}\))

Mà \(\widehat {ACB} = {60^0}\)  (vì \(∆ABC\) đều)

\( \Rightarrow \widehat {AMB} = {60^0}\) hay \(\widehat {DMB} = {60^0}\)

Vậy \(∆MBD\) đều

\(b)\) \(∆MBD\) đều

\( \Rightarrow \widehat {DBC} + \widehat {CBM} = \widehat {DBM} = {60^0}\)           \( (1)\)

\(∆ABC\) đều \( \Rightarrow \widehat {ABD} + \widehat {DBC} = \widehat {ABC} = {60^0}\)     \( (2)\)

Từ \((1)\) và \((2)\) suy ra: \(\widehat {CBM} = \widehat {ABD}\)

Xét \(∆BDA\) và \(∆BMC:\)

\(BA = BC \;\;(gt)\)

\(\widehat {ABD} = \widehat {CBM}\) (chứng minh trên)

\(BD = BM\) (vì \(∆MBD\) đều)

Suy ra: \(∆BDA = ∆BMC\;\; (c.g.c)\)

\(c)\) \(∆BDA = ∆BMC\) (chứng minh trên)

\( \Rightarrow DA = MC\)

Ta có: \(MB = MD\;\; (gt)\)  mà \(AM = AD + DM\)

Suy ra: \(MA = MB + MC \;\;(đpcm)\)

Loigiaihay.com