Bài 2 trang 113 Vở bài tập toán 7 tập 2

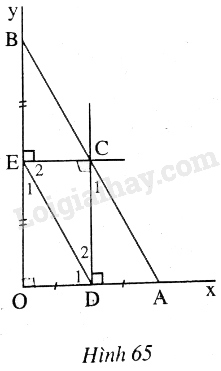
Đề bài

Cho góc vuông $xOy$, điểm $A$ thuộc tia $Ox$, điểm $B$ thuộc tia $Oy.$ Đường trung trực của đoạn thẳng $OA$ cắt $Ox$ ở $D$, đường thẳng trung trực của đoạn thẳng $OB$ cắt $Oy$ ở $E.$ Gọi $C$ là giao điểm của hai đường trung trực đó. Chứng minh rằng:

a) $CE = OD$;                b) $CE ⊥ CD$;

c) $CA = CB$;                 d) $CA // DE$;

e) Ba điểm $A, B, C$ thẳng hàng.

Lời giải chi tiết

 

a) Nối $ED$. Ta có  $EC // OD$ (vì cùng vuông góc với $OB$) nên $\widehat {E_2}$$= \widehat {D_1}$ (so le trong).

Tương tự, ta cũng có $DC // OE$ nên $\widehat {E_1}$$= \widehat {D_2}$.

Xét  $\Delta DOE$ và $\Delta ECD$, chúng có:

$\widehat {E_1}$$= \widehat {D_2}$; cạnh $DE$ chung; $\widehat {D_1}$$= \widehat {E_2}$

Do đó $\Delta DOE = \Delta ECD$  (g.c.g). Suy ra $CE=OD$.

b) Cũng do $\Delta DOE = \Delta ECD$ (chứng minh trên) ta còn suy ra $\widehat {O}$$= \widehat {ECD}$ mà $\widehat {O}=90^{\circ}$ nên $\widehat {ECD}=90^{\circ}$. Vậy $CE \perp CD$.

c) Xét $\Delta CDA$ và $\Delta BEC$. Chúng có :

$AD=CE,$ (cùng bằng $OD$); $\widehat {CDA}$$= \widehat {BEC}=90^{\circ}$, $CD=BE$ (cùng bằng $EO$ do $\Delta DOE = \Delta ECD$). Do đó $\Delta CDA$ $=\Delta BEC$ (c-g-c). Suy ra $CA=CB$.

d) Xét $\Delta CDA$ và $\Delta DCE$. Chúng có:

$AD = CE$, $\widehat {CDA} = \widehat {ECD} = 90^o$, cạnh $CD$ chung.

Do đó $∆CDA = ∆DCE$ (c.g.c) suy ra $\widehat {C_1} = \widehat {D_2}$. Do đó $CA // DE$ (vì có hai góc so le trong bằng nhau)

e) Tương tự câu d) ta có $CB // DE$. Như vậy qua điểm $C$ có $CA$ và $CB$ cùng song song với $DE$ nên theo tiên đề Ơclit, hai đường thẳng $CA$ và $CB$ trùng nhau. Do đó $A, B, C$ là ba điểm thẳng hàng.

Loigiaihay.com