Giải bài 14 trang 18 sách bài tập toán 9 - Chân trời sáng tạo tập 2

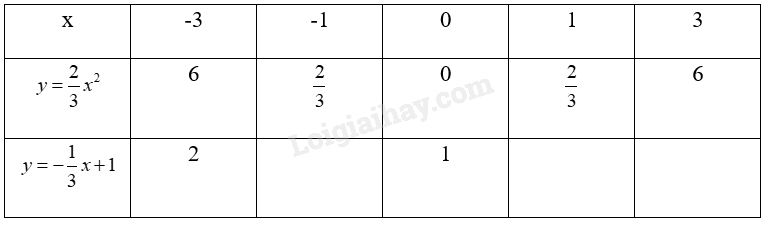
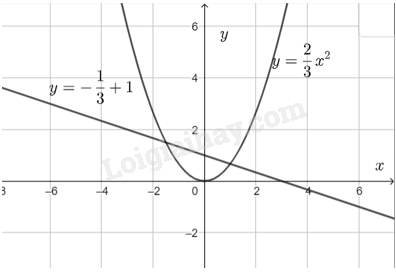
Đề bài

a) Vẽ đồ thị (P) của hàm số \(y = \frac{2}{3}{x^2}\) và đường thẳng d: \(y =  - \frac{1}{3}x + 1\) trên cùng một mặt phẳng toạ độ Oxy.

b) Tìm toạ độ giao điểm của (P) và d bằng phép tính.

Lời giải chi tiết

Bảng giá trị hàm số:

Đồ thị hàm số \(y = \frac{2}{3}{x^2}\) và đường thẳng d: \(y =  - \frac{1}{3}x + 1\) được biểu thị dưới đây:

b) Giao điểm của (P) và d là điểm có hoành độ thoả mãn phương trình

 \(\begin{array}{l}\frac{2}{3}{x^2} =  - \frac{1}{3}x + 1\\\frac{2}{3}{x^2} + \frac{1}{3}x - 1 = 0\end{array}\)

Giải phương trình trên, ta được \({x_1} = 1;{x_2} =  - \frac{3}{2}\).

Thay x = 1 vào \(y = \frac{2}{3}{x^2}\), ta được \(y = \frac{2}{3}{.1^2} = \frac{2}{3}\).

Thay \(x =  - \frac{3}{2}\) vào \(y = \frac{2}{3}{x^2}\), ta được \(y = \frac{2}{3}.{\left( { - \frac{3}{2}} \right)^2} = \frac{3}{2}\).

Vậy toạ độ giao điểm của (P) và d là \(\left( {1;\frac{2}{3}} \right)\) và \(\left( { - \frac{3}{2};\frac{3}{2}} \right)\).