Giải bài 11 trang 84 sách bài tập toán 9 - Cánh diều tập 1

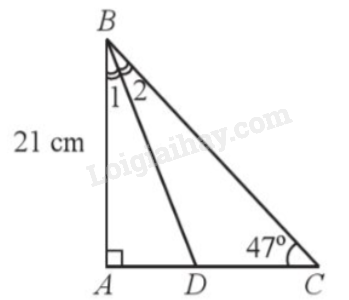
Đề bài

Cho tam giác ABC vuông tại A có AB = 21cm, \(\widehat C = 47^\circ \). Tính độ dài đường phân giác BD của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet).

Lời giải chi tiết

Xét tam giác vuông ABC, ta có:

\(\widehat {ABC} = 90^\circ  - \widehat C = 90^\circ  - 47^\circ  = 43^\circ .\)

Mà BD là đường phân giác của tam giác ABC nên

\(\widehat {{B_1}} = \widehat {{B_2}} = \frac{{\widehat {ABC}}}{2} = \frac{{43^\circ }}{2} = 21,5^\circ \).

Xét tam giác ABD vuông tại A, ta có \(\cos \widehat {{B_1}} = \frac{{AB}}{{BD}}\) hay \(\cos 21,5^\circ  = \frac{{21}}{{BD}}\).

Suy ra \(BD = \frac{{21}}{{\cos 21,5^\circ }} \approx 22,57\)cm.

Vậy BD = 22,57cm.