Giải bài 14 trang 85 sách bài tập toán 9 - Cánh diều tập 1Chứng minh diện tích tam giác đều cạnh a là \(\frac{{{a^2}\sqrt 3 }}{4}\). Quảng cáo
Đề bài Chứng minh diện tích tam giác đều cạnh a là \(\frac{{{a^2}\sqrt 3 }}{4}\). Phương pháp giải - Xem chi tiết Bước 1: Áp dụng tỉ số lượng giác trong tam giác vuông ABH để tính AH. Bước 2: \({S_{ABC}} = \frac{1}{2}AH.BC\) Lời giải chi tiết
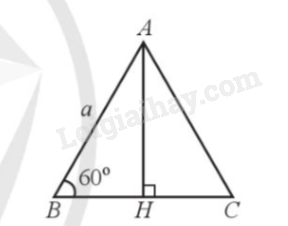
Giả sử ta có tam giác ABC đều, cạnh a, đường cao AH. Xét tam giác vuông ABH có \(\sin B = \frac{{AH}}{{AB}}\) hay \(AH = AB.\sin B = a.\sin 60^\circ = \frac{{a\sqrt 3 }}{2}\). Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^2}\sqrt 3 }}{4}\)(đvdt) Vậy diện tích tam giác đều cạnh a là \(\frac{{{a^2}\sqrt 3 }}{4}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
