Giải bài 13 trang 85 sách bài tập toán 9 - Cánh diều tập 1

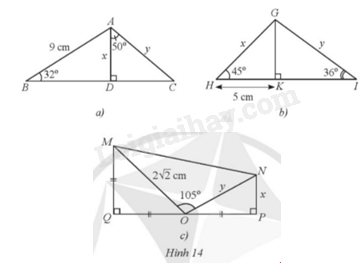
Đề bài

Tìm x, y trong mỗi hình 14a, 14b, 14c (làm tròn kết quả đến hàng phần mười của centimet).

Lời giải chi tiết

a) Xét tam giác ABD vuông tại D, ta có

\(\sin B = \frac{{AD}}{{AB}}\) hay \(\sin 32^\circ  = \frac{x}{9}\),

do đó \(x = 9.\sin 32^\circ  \approx 4,8\)cm.

Xét tam giác ACD vuông tại D, ta có

\(\cos \widehat {DAC} = \frac{{AD}}{{AC}}\) hay \(\cos 50^\circ  = \frac{{4,8}}{y}\),

do đó \(y = \frac{{4,8}}{{\cos 50^\circ }} \approx 7,5\)cm.

b) Xét tam giác GHK vuông tại K, \(\widehat H = 45^\circ \) nên đây là tam giác vuông cân,

 suy ra HK = GK = 5cm, và \(\sin I = \frac{{GK}}{{GI}}\) hay \(\sin 36^\circ  = \frac{5}{y}\),

do đó \(y = \frac{5}{{\sin 36^\circ }} \approx 8,5\)cm.

c) Xét tam giác MOQ có \(\widehat Q = 90^\circ ,MQ = QO\) nên tam giác MOQ vuông cân tại Q.

Do đó \(M{Q^2} + Q{O^2} = M{O^2}\) hay \(2Q{O^2} = {\left( {2\sqrt 2 } \right)^2}\), nên \(QO = 2\)cm = OP.

Ta lại có tam giác MOQ vuông cân tại Q nên \(\widehat {QOM} = 45^\circ \).

Mặt khác \(\widehat {QOM} + \widehat {MON} + \widehat {NOP} = 45^\circ  + 105^\circ  + \widehat {NOP} = 180^\circ \), suy ra \(\widehat {NOP} = 30^\circ \)

Xét tam giác vuông NOP có

\(\tan \widehat {NOP} = \frac{{NP}}{{OP}}\) hay \(NP = x = \tan \widehat {NOP}.OP = \tan 30^\circ .2 \approx 1,2\)cm.

Và \(\cos \widehat {NOP} = \frac{{OP}}{{ON}}\) hay \(ON = y = \frac{{OP}}{{\cos \widehat {NOP}}} = \frac{2}{{\cos 30^\circ }} \approx 2,3\)cm.