Giải bài 12 trang 85 sách bài tập toán 9 - Cánh diều tập 1Cho tam giác ABC có AB = 6cm, \(\widehat A = 15^\circ ,\widehat B = 35^\circ \). Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet). Quảng cáo
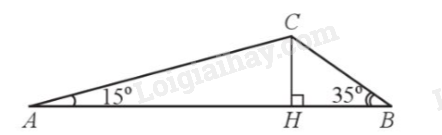
Đề bài Cho tam giác ABC có AB = 6cm, \(\widehat A = 15^\circ ,\widehat B = 35^\circ \). Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet). Phương pháp giải - Xem chi tiết Bước 1: Biểu diễn AH qua tanA và BH qua tanB. Bước 2: Thay AH, BH vào \(AB = AH + BH\), ta tìm được CH. Lời giải chi tiết
Do CH là đường cao của tam giác ABC nên \(\widehat {CHB} = \widehat {CHA} = 90^\circ \). Xét tam giác vuông CHA ta có \(\tan A = \frac{{CH}}{{AH}}\), do đó \(AH = \frac{{CH}}{{\tan A}}\). Xét tam giác vuông CHB ta có \(\tan B = \frac{{CH}}{{BH}}\), do đó \(BH = \frac{{CH}}{{\tan B}}\). Mặt khác \(AB = AH + BH\), suy ra \(\frac{{CH}}{{\tan A}} + \frac{{CH}}{{\tan B}} = 6\) hay \(\frac{{CH}}{{\tan 15^\circ }} + \frac{{CH}}{{\tan 35^\circ }} = 6\) Nên \(CH.\left( {\frac{1}{{\tan 15^\circ }} + \frac{1}{{\tan 35^\circ }}} \right) = 6\) suy ra \(CH = \frac{6}{{\left( {\frac{1}{{\tan 15^\circ }} + \frac{1}{{\tan 35^\circ }}} \right)}} \approx 1,16\left( {cm} \right)\) Vậy \(CH \approx 1,16\)cm.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
