Bài 11 trang 49 SBT toán 9 tập 2

LG a

Xác định hệ số \(a\) biết rằng đồ thị của nó cắt đường thẳng \(y =  - 2x + 3\) tại điểm \(A\) có hoành độ bằng \(1.\)

Phương pháp giải:

+) Thay tọa độ điểm mà đồ thị đi qua vào hàm số, từ đó ta tìm được hệ số.

Lời giải chi tiết:

Điểm \(A\) thuộc đồ thị hàm số \(y =  - 2x + 3\) nên tọa độ của \(A\) nghiệm đúng phương trình đường thẳng: \(y =  - 2x + 3\)

Suy ra \(y =  - 2.1 + 3 = 1\) điểm \(A (1; 1)\)

Điểm \(A (1; 1)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên tọa độ của điểm \(A\) thỏa mãn hàm số \(y = a{x^2}\)

Nên ta có: \(1 = a{.1^2} \Leftrightarrow a = 1\)

Hàm số đã cho: \(y = {x^2}\)

LG b

Vẽ đồ thị của hàm số \(y =  - 2x + 3\) và của hàm số \(y = a{x^2}\) với giá trị của \(a\) vừa tìm được trong câu \(a\) trên cùng một mặt phẳng tọa độ.

Phương pháp giải:

+) Để vẽ đồ thị hàm số: ta lấy một số điểm đồ thị hàm số đi qua rồi từ đó vẽ đồ thị.

Lời giải chi tiết:

Vẽ đồ thị hàm số: \(y = {x^2}\)

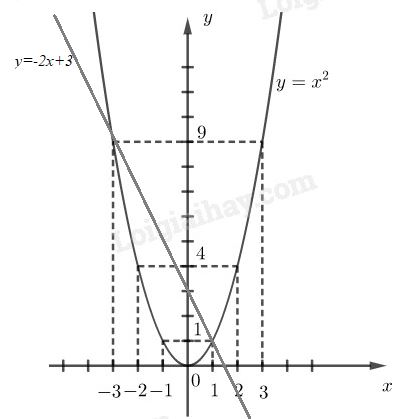
Vẽ đồ thị \(y =  - 2x + 3\)

Cho \(x = 0 \Rightarrow y = 3\) suy ra  \(B (0; 3)\)

Cho \(x = 1 \Rightarrow y = 1\)  suy ra \(A (1; 1)\)

Khi đó, đồ thị hàm số \(y =  - 2x + 3\) là đường thẳng đi qua hai điểm \(A,B\)

Vẽ hình:

LG c

Nhờ đồ thị xác định tọa độ của giao điểm thứ hai của hai đồ thị vừa vẽ trong câu \(b.\)

Phương pháp giải:

Quan sát đồ thị hàm số rồi kết luận

Lời giải chi tiết:

Giao điểm thứ hai \(A’\) của đường thẳng và parabol có hoành độ \(x = -3;\) tung độ \(y = 9\) suy ra \(A’ (-3; 9)\)

Loigiaihay.com