Bài 10 trang 197 SBT toán 9 tập 2

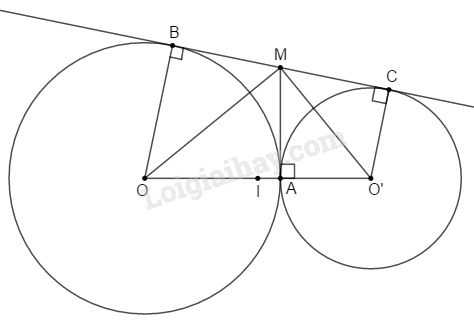
Đề bài

Cho hai đường tròn \((O;16cm)\) và \((O';9cm)\) tiếp xúc ngoài tại \(A\). Gọi \(BC\) là tiếp tuyến chung ngoài của hai đường tròn \((B\in (O), C\in (O'))\). Kẻ tiếp tuyến chung tại \(A\) cắt \(BC\) ở \(M\).

a) Tính góc \(OMO'\).

b) Tính độ dài \(BC\).

c) Gọi \(I\) là trung điểm của \(OO'\). Chứng minh rằng \(BC\) là tiếp tuyến của đường tròn tâm \(I\), bán kính \(IM\).

Lời giải chi tiết

a) \(MO\) là tia phân giác của \(\widehat {AMB}\) (tính chất hai tiếp tuyến cắt nhau).

\( \Rightarrow \widehat {BMO} = \widehat {OMA} = \dfrac{1}{2}\widehat {AMB}\)

\(MO'\) là tia phân giác của \(\widehat {AMC}\) (tính chất hai tiếp tuyến cắt nhau).

\( \Rightarrow \widehat {CMO'} = \widehat {O'MA} = \dfrac{1}{2}\widehat {AMC}\)

Ta có: \(\widehat {OMO'} = \widehat {OMA} + \widehat {O'MA} \)

\( \Rightarrow \widehat {OMO'}= \dfrac{1}{2}\widehat {AMB} + \dfrac{1}{2}\widehat {AMC} \)\(\,= \dfrac{1}{2}\left( {\widehat {AMB} + \widehat {AMC}} \right)\)\(\, = \dfrac{1}{2}{.180^o} = {90^o}\)

b) Xét \(\Delta OMO'\) vuông tại \(M\) ta có:

\(\begin{array}{l}
M{A^2} = OA.O'A = 16.9 = 144\\
\Rightarrow MA = \sqrt {144} = 12\,\left( {cm} \right).
\end{array}\)

Lại có \(MA=MB=MC\) (tính chất hai tiếp tuyến cắt nhau).

\( \Rightarrow MB = MC = 12\,\left( {cm} \right).\)

\( \Rightarrow BC = MB + MC = 12 + 12 \)\(\,= 24\,\left( {cm} \right).\)

c) 

\(\left. \begin{array}{l}
OB \bot BC\\
O'C \bot BC
\end{array} \right\} \Rightarrow OB//O'C\)

Do đó tứ giác \(OBCO'\) là hình thang.

Có \(MB=MC;IA=IB\) nên \(IM\) là đường trung bình của hình thang \(OBCO'\). Do đó \(IM//OB//O'C\).

Mà \(OB\bot BC\) nên \(IM\bot BC\).

\(\Delta OMO'\) vuông tại \(M\) có \(IM\) là trung tuyến ứng với cạnh huyền nên \(IM = \dfrac{1}{2}OO'\).

Do đó \(IM\) là bán kính của đường tròn tâm \(I\) lại vuông góc với \(BC\) tại \(M\) nên \(BC\) là tiếp tuyến của \((I;IM)\).

Loigiaihay.com