Giải bài 1 trang 36 sách bài tập toán 12 - Chân trời sáng tạoGiá thành của một sản phẩm trong 6 tháng đầu năm thay đổi theo công thức (Pleft( t right) = 2{t^3} - 33{t^2} + 168t + 137) với (P) tính bằng nghìn đồng và (t) là số tháng tính từ đầu năm. Trong khoảng thời gian nào thì giá của sản phẩm tăng? Quảng cáo
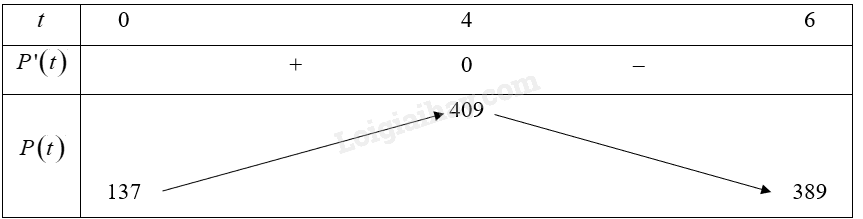
Đề bài Giá thành của một sản phẩm trong 6 tháng đầu năm thay đổi theo công thức \(P\left( t \right) = 2{t^3} - 33{t^2} + 168t + 137\) với \(P\) tính bằng nghìn đồng và \(t\) là số tháng tính từ đầu năm. Trong khoảng thời gian nào thì giá của sản phẩm tăng? Phương pháp giải - Xem chi tiết Xét hàm số \(P\left( t \right)\) trên đoạn \(\left[ {0;6} \right]\), lập bảng biến thiên và tìm khoảng đồng biến của hàm số. Lời giải chi tiết Xét hàm số \(P\left( t \right) = 2{t^3} - 33{t^2} + 168t + 137\) trên đoạn \(\left[ {0;6} \right]\). Ta có: \(P'\left( t \right) = 6{t^2} - 66t + 168;P'\left( t \right) = 0 \Leftrightarrow t = 4\) hoặc \(t = 7\) (loại). Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng \(\left( {0;4} \right)\). Vậy trong khoảng thời gian 4 tháng đầu năm thì giá của sản phẩm tăng.
|




















Danh sách bình luận