Đề thi vào lớp 6 môn Toán trường THCS Nam Từ Liêm năm 2024Tải vềThầy Cường gửi tiết kiệm 50 triệu đồng với lãi suất 6%/năm Một xe đạp đi từ A đến C với vận tốc 12km/giờ. Sau khi đi được 1 giờ 30 phút có một xe máy đi từ A đến C với vận tốc 36km/giờ đuổi theo xe đạp Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
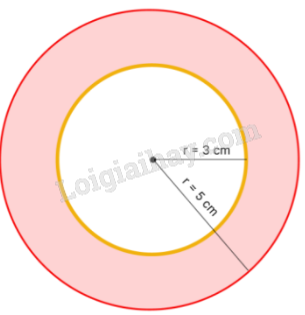
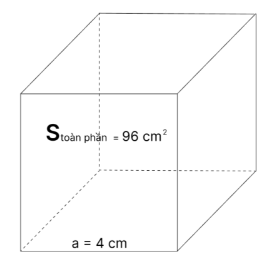
Đề bài PHẦN 1. TRẮC NGHIỆM Câu 1. Tính giá trị biểu thức: 12,6 + 9,3 + 25,4 – 6,3 Câu 2. Có bao nhiêu chữ số a thoả mãn $\overline {a31a5} $ chia hết cho 3? Câu 3. Điểm trung bình của 2 môn: Toán, Tiếng Việt là 7,5 điểm. Hỏi môn Tiếng Anh phải đạt bao nhiêu điểm để điểm trung bình của cả 3 môn là 8 điểm? Câu 4. Tổng số tuổi của hai bố con là 52 tuổi. Biết 2 năm trước tuổi con bằng $\frac{1}{7}$ tuổi bố. Tính tuổi con hiện nay? Câu 5. Tính thể tích hình lập phương có diện tích toàn phần là 96 cm2. Câu 6. Thầy Cường gửi tiết kiệm 50 triệu đồng với lãi suất 6%/năm. Hỏi sau 1 năm thầy Cường nhận được bao nhiêu tiền cả gốc và lãi? Câu 7. Cho hình biên, biết bán kính hình tròn nhỏ là 3 cm, bán kính hình tròn lớn là 5 cm. Tính diện tích hình tô đậm.
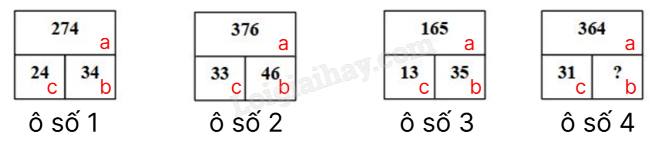
Câu 8. Trong hộp chứahai loại bi, bi xanh và bi đỏ. Biết số bi xanh chiếm 60% số bi của cả hộp và hiệu số bi 2 loại là 12 viên. Tính số bi đỏ? Câu 9. Ngày 7/5/2024 là thứ Ba, hỏi ngày này 4 năm sau là thứ mấy? Câu 10. Điền số thích hợp vào dấu hỏi chấm (?).
PHẦN 2. TỰ LUẬN Bài 1. 1) Tìm $x$ biết $\left( {x + \frac{2}{3}} \right) \times \frac{9}{{15}} = 2\frac{1}{3} - \frac{8}{6}$ 2) Một xe đạp đi từ A đến C với vận tốc 12km/giờ. Sau khi đi được 1 giờ 30 phút có một xe máy đi từ A đến C với vận tốc 36km/giờ đuổi theo xe đạp. Hỏi: a) Sau bao lâu xe máy đuổi kịp xe đạp? b) Sau khi gặp nhau, xe đạp quay trở về A ngay còn xe máy nghỉ lại 30 phút rồi tiếp tục quay về A. Hỏi khi trở về A, xe máy gặp xe đạp tại điểm cách A bao nhiêu ki-lô-mét? Bài 2. Cho hình vuông ABCD có cạnh 10 cm. Điểm M trên cạnh AD sao cho $AM = \frac{2}{5}AD$. O là giao điểm của BM và AC. Nối M với C. 1) Tính diện tích tam giác ABM. 2) Tính $\frac{{{S_{BMC}}}}{{{S_{ABM}}}}$ ? 3) Tính $\frac{{BO}}{{OM}}$
Bài 3. Có hai giỏ, mỗi giỏ đựng 1 loại quả táo hoặc quả lê. - Mai nói: “2 quả táo nặng hơn 3 quả lê”. - Lan nói: “3 quả táo nặng hơn 4 quả lên”. Biết rằng chỉ có 1 bạn nói đúng. Hỏi ai là người nói đúng?
Đáp án HƯỚNG DẪN GIẢI CHI TIẾT PHẦN 1. TRẮC NGHIỆM Câu 1. Tính giá trị biểu thức: 12,6 + 9,3 + 25,4 – 6,3 Lời giải 12,6 + 9,3 + 25,4 – 6,3 = (12,6 + 25,4) + (9,3 – 6,3) = 38 + 3 = 41 Đáp số: 41 Câu 2. Có bao nhiêu chữ số a thoả mãn $\overline {a31a5} $ chia hết cho 3? Lời giải $\overline {a31a5} $ chia hết cho 3 nên ta có: a + 3 + 1 + a + 5 = a × 2 + 9 chia hết cho 3 hay a × 2 chia hết cho 3 Suy ra: a = 0; 3; 6; 9. Do a khác 0 nên có 3 giá trị thoả mãn: 3; 6; 9 Đáp số: 3; 6; 9 Câu 3. Điểm trung bình của 2 môn: Toán, Tiếng Việt là 7,5 điểm. Hỏi môn Tiếng Anh phải đạt bao nhiêu điểm để điểm trung bình của cả 3 môn là 8 điểm? Lời giải Tổng điểm Toán và Tiếng Việt là: 7,5 × 2 = 15 (điểm) Tổng điểm Toán, Tiếng Việt và Tiếng Anh là: 8 × 3 = 24 (điểm) Điểm Tiếng Anh cần đạt được là: 24 – 15 = 9 (điểm) Đáp số: 9 điểm Câu 4. Tổng số tuổi của hai bố con là 52 tuổi. Biết 2 năm trước tuổi con bằng $\frac{1}{7}$ tuổi bố. Tính tuổi con hiện nay? Lời giải Tổng số tuổi của hai bố con 2 năm trước là: 52 – 2 × 2 = 48 (tuổi) Tuổi con 2 năm trước là: 48 : (7 + 1) x 1 = 6 (tuổi) Tuổi con hiện nay là: 6 + 2 = 8 (tuổi) Đáp số: 8 tuổi Câu 5. Tính thể tích hình lập phương có diện tích toàn phần là 96 cm2. Lời giải
Diện tích 1 mặt hình lập phương là: 96 : 6 = 16 (cm2) Ta có: 4 × 4 = 16 nên 1 cạnh hình lập phương là: 4 (cm) Thể tích hình lập phương là: 4 × 4 × 4 = 65 (cm3) Đáp số: 65 cm3 Câu 6. Thầy Cường gửi tiết kiệm 50 triệu đồng với lãi suất 6%/năm. Hỏi sau 1 năm thầy Cường nhận được bao nhiêu tiền cả gốc và lãi? Lời giải Số tiền lãi sau 1 năm là: 50 000 000 × 6 : 100 = 3 000 000 (đồng) Sau 1 năm số tiền thầy Cường nhận về cả gốc và lãi là: 50 000 000 + 3 000 000 = 53 000 000 (đồng) Đáp số: 53 000 000 đồng Câu 7. Cho hình biên, biết bán kính hình tròn nhỏ là 3 cm, bán kính hình tròn lớn là 5 cm. Tính diện tích hình tô đậm.
Lời giải Ta nhận thấy diện tích hình tô màu bằng diện tích hình tròn lớn trừ đi diện tích hình tròn nhỏ. Diện tích hình tròn nhỏ: 3 × 3 × 3,14 = 28,26 (cm2) Diện tích hình tròn lớn là: 5 × 5 × 3,14 = 78,5 (cm2) Diện tích phần tô màu: 78,5 – 28,26 = 50,24 (cm2) Đáp số: 50,24 cm2 Câu 8. Trong hộp chứa hai loại bi, bi xanh và bi đỏ. Biết số bi xanh chiếm 60% số bi của cả hộp và hiệu số bi 2 loại là 12 viên. Tính số bi đỏ? Lời giải Ta có 60% = $\frac{3}{5}$ Số bi xanh bằng $\frac{3}{5}$ tổng số bi hay số bi xanh bằng: $\frac{3}{{5 - 3}} = \frac{3}{2}$ số bi đỏ Số bi đỏ là: 12 : (3 – 2) × 2 = 24 (viên bi) Đáp số: 24 viên bi Câu 9. Ngày 7/5/2024 là thứ Ba, hỏi ngày này 4 năm sau là thứ mấy? Lời giải Từ 7/5/2024 đến 7/5 của 4 năm sau có: 365 × 4 + 1 = 1461 ngày Ta có: 1461 : 7 = 208 (dư 5). Do vậy ngày 7/5 của 4 năm nữa là chủ nhật Đáp số: chủ nhật Câu 10. Điền số thích hợp vào dấu hỏi chấm (?).
Lời giải Ta đánh thứ tự các ô số nhỏ từng ô số một như hình.
Ta nhận thấy Quy Luật chung của 4 ô số đó là: Lấy (a – b) : 10 = c Ta có: Ô số 1: (274 – 34 ) : 10 = 24 Ô số 2: (376 – 46) : 10 = 33 Ô số 3: (165 – 35) : 10 = 13 Ô số 4: (364 - b) : 10 = 31 364 – b = 31 × 10 b = 364 – 310 = 54 Đáp số: 54 PHẦN 2. TỰ LUẬN Bài 1.
1) Tìm $x$ biết $\left( {x + \frac{2}{3}} \right) \times \frac{9}{{15}} = 2\frac{1}{3} - \frac{8}{6}$ 2) Một xe đạp đi từ A đến C với vận tốc 12km/giờ. Sau khi đi được 1 giờ 30 phút có một xe máy đi từ A đến C với vận tốc 36km/giờ đuổi theo xe đạp. Hỏi: a) Sau bao lâu xe máy đuổi kịp xe đạp? b) Sau khi gặp nhau, xe đạp quay trở về A ngay còn xe máy nghỉ lại 30 phút rồi tiếp tục quay về A. Hỏi khi trở về A, xe máy gặp xe đạp tại điểm cách A bao nhiêu ki-lô-mét? Lời giải 1) $\left( {x + \frac{2}{3}} \right) \times \frac{9}{{15}} = 2\frac{1}{3} - \frac{8}{6}$ $\left( {x + \frac{2}{3}} \right) \times \frac{3}{5} = \frac{7}{3} - \frac{4}{3}$ $\left( {x + \frac{2}{3}} \right) \times \frac{3}{5} = 1$ $x + \frac{2}{3} = 1:\frac{3}{5}$ $x + \frac{2}{3} = \frac{5}{3}$ $x = \frac{5}{3} - \frac{2}{3}$ $x = 1$ 2) Đổi: 1 giờ 30 phút = 1,5 giờ Khi xe máy xuất phát, xe đạp đã đi được quãng đường dài là: 12 x 1,5 = 18 (km) b) 18km Bài 2. Cho hình vuông ABCD có cạnh 10 cm. Điểm M trên cạnh AD sao cho $AM = \frac{2}{5}AD$. O là giao điểm của BM và AC. Nối M với C. 1) Tính diện tích tam giác ABM. 2) Tính $\frac{{{S_{BMC}}}}{{{S_{ABM}}}}$ ? 3) Tính $\frac{{BO}}{{OM}}$
Lời giải a) Vì ABCD là hình vuông cạnh 10cm nên AB = BC = CD = DA = 10 cm. Ta có $AM = \frac{2}{5}AD = \frac{2}{5} \times 10 = 4$ (cm) Diện tích tam giác ABM là: 4 × 10 : 2 = 20 (cm2) b) $\frac{{{S_{CMB}}}}{{{S_{BMA}}}} = \frac{{BC}}{{AM}} = \frac{5}{2}$ (do hai chiều cao bằng nhau và bằng cạnh hình vuông; BC = AD = $\frac{5}{2}$ AM) c) Xét 2 tam giác AMB và BMC: có chung đáy MB Mà $\frac{{{S_{CMB}}}}{{{S_{BMA}}}} = \frac{5}{2}$ nên chiều cao hạ từ C xuống MB bằng $\frac{5}{2}$ chiều cao hạ từ A xuống MB. Ta có $\frac{{{S_{MOC}}}}{{{S_{MOA}}}} = \frac{5}{2}$ (do chung đáy MO) (1) Ta có ${S_{AMB}} = {S_{AMC}}$(chiều cao bằng nhau và bằng cạnh hình vuông; chung đáy AM) Nên SAMB – SAMO = SAMC – SAMO hay SAOB = SMOC (2) Từ (1) và (2) suy ra $\frac{{{S_{AOB}}}}{{{S_{MOA}}}} = \frac{5}{2}$ Mà hai tam giác có chung chiều cao hạ từ A xuống MB nên $\frac{{BO}}{{OM}} = \frac{5}{2}$ Bài 3. Có hai giỏ, mỗi giỏ đựng 1 loại quả táo hoặc quả lê. - Mai nói: “2 quả táo nặng hơn 3 quả lê”. - Lan nói: “3 quả táo nặng hơn 4 quả lên”. Biết rằng chỉ có 1 bạn nói đúng. Hỏi ai là người nói đúng? Lời giải Mai nói: “2 quả táo nặng hơn 3 quả lê” nên 6 quả táo nặng hơn 9 quả lê. Lan nói : “3 quả táo nặng hơn 4 quả lê” nên 6 quả táo nặng hơn 8 quả lê. Giả sử: Mai nói đúng thì Lan cũng nói đúng vì 6 quả táo > 9 quả lê > 8 quả lên. Vậy theo trường hợp này cả hai đều đúng. Trong khi đó, đề bài cho chỉ một người nói đúng nên mâu thuẫn. Do đó, Lan là người nói đúng.
|

























Danh sách bình luận