Đề thi vào lớp 6 môn Toán trường Nam Từ Liêm năm 2022Tải vềDiện tích toàn phần hình lập phương hơn diện tích xung quang là 18 cm2 ... Có một dãy nhà người ta đánh số lẻ từ 1 đến 29 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG THCS NAM TỪ LIÊM NĂM HỌC 2022 – 2023 Thời gian làm bài: 50 phút PHẦN 1. TRẮC NGHIỆM Câu 1. 126 x 9,8 + 126 x 0,7 – 126 x 0,5 Câu 2. Diện tích toàn phần hình lập phương hơn diện tích xung quang là 18 cm2. Tính thể tích hình lập phương? Câu 4. Phân số nào bé nhất $\frac{5}{6}$ ; $\frac{{2021}}{{2022}}$ ; $\frac{{2020}}{{2021}}$ ; $\frac{3}{4}$ ; $\frac{3}{2}$ Câu 5. Tìm $x$: $60:x - \frac{1}{3} = 4\frac{2}{3}$ Câu 6. Lớp 5A có 50 học sinh, $\frac{2}{5}$ học sinh thích đá bóng; 16% thích đá cầu, 24% thích bóng rổ còn lại thích cầu lông. Hỏi có bao nhiêu học sinh thích cầu lông?
PHẦN 2. TỰ LUẬN Câu 1. Có hai xe đi cùng chiều với nhau về phía C. Quãng đường AB dài 60 km (B nằm giữa AC). Hai người gặp nhau sau 6 giờ. Câu 2. Cho hình chữ nhật ABCD, biết BM = MC, SABCD = 60 cm2, SMNC = 10 cm2
a) Tính diện tích tam giác DMC. b) Tính tỉ số $\frac{{MN}}{{DN}}$ c) Tính tỉ số $\frac{{{S_{NDP}}}}{{{S_{NPC}}}}$ Đáp án HƯỚNG DẪN GIẢI CHI TIẾT PHẦN 1. TRẮC NGHIỆM Câu 1. 126 x 9,8 + 126 x 0,7 – 126 x 0,5 Hướng dẫn: 126 x 9,8 + 126 x 0,7 – 126 x 0,5 = 1260 Đáp số: 1260 Câu 2. Diện tích toàn phần hình lập phương hơn diện tích xung quang là 18 cm2. Tính thể tích hình lập phương? Hướng dẫn: Gọi độ dài cạnh của hình lập phương là a Ta có a x a x 6 – a x a x 4 = 18 $ \Rightarrow $a x a x 2 = 18 $ \Rightarrow $a x a = 9 Vậy độ dài cạnh hình vuông là 3 cm. Thể tích hình lập phương là 3 x 3 x 3 = 27 (cm3) Đáp số: 27cm3 Hướng dẫn: Gọi số cần tìm là $\overline {ab} $ (a khác 0; a , b < 10) Ta có $\overline {ab2} = \overline {ab} + 335$ $\overline {ab} \times 10 + 2 = \overline {ab} + 335$ $\overline {ab} \times 9 = 333$ $\overline {ab} = 333:9$ $\overline {ab} = 37$ Đáp số: 37 Câu 4. Phân số nào bé nhất $\frac{5}{6}$ ; $\frac{{2021}}{{2022}}$ ; $\frac{{2020}}{{2021}}$ ; $\frac{3}{4}$ ; $\frac{3}{2}$ Hướng dẫn: Ta có $\frac{5}{6} < 1$ ; $\frac{{2021}}{{2022}} < 1$ ; $\frac{{2020}}{{2021}} < 1$ ; $\frac{3}{4} < 1$ ; $\frac{3}{2} > 1$ Để tìm phân số bé nhất, ta chỉ việc so sánh các phân số < 1 Lại có: $1 - \frac{5}{6} = \frac{1}{6}$ ; $1 - \frac{{2021}}{{2022}} = \frac{1}{{2022}}$ ; $1 - \frac{{2020}}{{2021}} = \frac{1}{{2021}}$ ; $1 - \frac{3}{4} = \frac{1}{4}$ Vì $\frac{1}{4} > \frac{1}{6} > \frac{1}{{2021}} > \frac{1}{{2022}}$ nên $\frac{3}{4} < \frac{5}{6} < \frac{{2020}}{{2021}} < \frac{{2021}}{{2022}}$ Vậy phân số bé nhất là $\frac{3}{4}$ Đáp số: $\frac{3}{4}$ Câu 5. Tìm $x$ biết $60:x - \frac{1}{3} = 4\frac{2}{3}$ Hướng dẫn: $60:x - \frac{1}{3} = 4\frac{2}{3}$ $60:x = 4\frac{2}{3} + \frac{1}{3}$ $60:x = 5$ $x = 60:5$ $x = 12$ Đáp số: x = 12 Câu 6. Lớp 5A có 50 học sinh, $\frac{2}{5}$ học sinh thích đá bóng; 16% thích đá cầu, 24% thích bóng rổ còn lại thích cầu lông. Hỏi có bao nhiêu học sinh thích cầu lông? Hướng dẫn: Ta có $\frac{2}{5} = 0,4 = 40\% $ Số học sinh thích cầu lông chiếm số phần trăm là: 100% - (40% + 16% + 24%) = 20% (số học sinh cả lớp) Số học sinh thích cầu lông là: 50 x 20% = 10 (học sinh) Đáp số: 10 học sinh Hướng dẫn: Nam đến sớm hơn thời gian hẹn là: 9 giờ 10 phút – 8 giờ 50 phút = 20 phút Nam phải chờ Tùng số phút là: 20 phút + 18 phút = 38 (phút) Đáp số: 38 phút Hướng dẫn: Tổng hai số là 85 x 2 = 170 Số lớn là (170 + 20) : 2 = 95 Đáp số: 95 Hướng dẫn: Tổng số tuổi của hai em hiện nay là: 11 + 5 = 16 (tuổi) Số năm để tổng số tuổi hai anh em là 28 tuổi là: (28 – 16) : 2 = 6 (tuổi) Đáp số: 6 năm Hướng dẫn: Từ nhà số 1 đến nhà số 9 có 5 nhà Từ số nhà 11 đến số nhà 29 có: (29 – 11): 2 + 1 = 10 (nhà) Đáp số: 750 000 đồng
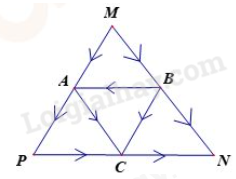
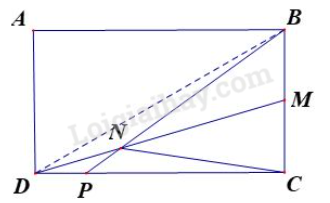
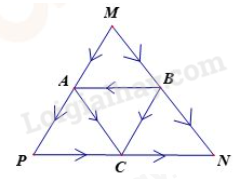
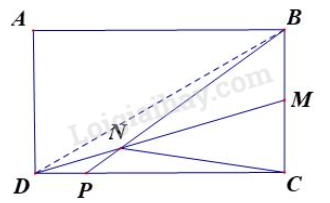
Hướng dẫn: Các cách con kiến đi từ M đến N: Cách 1: MBN Cách 2: MBCN Cách 3: MBACN Cách 4: MBAPCN Cách 5: MACN Cách 6: MAPCN Đáp số: 6 cách PHẦN 2. TỰ LUẬN Câu 1. Có hai xe đi cùng chiều với nhau về phía C. Quãng đường AB dài 60 km (B nằm giữa AC). Hai người gặp nhau sau 6 giờ. Hướng dẫn: a, Hiệu vận tốc hai xe ô tô là: 60 : 6 = 10 (km/giờ) Câu 2. Cho hình chữ nhật ABCD, biết BM = MC, SABCD = 60 cm2, SMNC = 10 cm2
a) Tính diện tích tam giác DMC. b) Tính tỉ số $\frac{{MN}}{{DN}}$ c) Tính tỉ số $\frac{{{S_{NDP}}}}{{{S_{NPC}}}}$ Hướng dẫn: a) SDMC = MC x CD x $\frac{1}{2}$ = $\frac{1}{2} \times BC \times CD \times \frac{1}{2}$ =$\frac{1}{4}$ x SABCD = $\frac{1}{4} \times 60 = 15$ (cm2) b) SDNC = SDMC - SNMC = 15 – 10 = 5 (cm2) $\frac{{{S_{NMC}}}}{{{S_{DNC}}}} = \frac{{10}}{5} = 2$ Ta thấy hai tam giác NMC và DNC có chung chiều cao hạ từ đỉnh C $ \Rightarrow $$\frac{{MN}}{{DN}} = 2$ c) SDBM = SDMC (Chung đường cao hạ từ D và đáy BM = MC) Mà SNMB = SNMC (Chung đường cao hạ từ N và đáy BM = MC) Suy ra SDNB = SDNC = 5 cm2 Lại có $\frac{{{S_{DNB}}}}{{{S_{BNC}}}} = \frac{5}{{10 + 10}} = \frac{1}{4}$ Suy ra đường cao hạ từ D xuống đáy BN = $\frac{1}{4}$ đường cao hạ từ C xuống đáy BN Vậy $\frac{{{S_{NDP}}}}{{{S_{NPC}}}} = \frac{1}{4}$ (Chung đáy NP và đường cao hạ từ D xuống đáy NP = $\frac{1}{4}$ đường cao hạ từ C xuống đáy NP)
|




















Danh sách bình luận