Đề thi vào lớp 6 môn Toán trường Amsterdam năm 2020Tải vềCho một hình chữ nhật có chu vi 160cm, sau khi cùng giảm chiều dài và rộng đi cùng một độ dài thì hình mới có chu vi 120cm .... Cho một hình hộp chữ nhật. Người ta tăng chiều dài của hình hộp chữ nhật 10% và giảm chiều rộng của nó đi 20% Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài ĐỀ THI TUYỂN SINH VÀO LỚP 6 MÔN TOÁN TRƯỜNG AMSTERDAM NĂM HỌC 2020 – 2021
PHẦN 1. TRẮC NGHIỆM
PHẦN 2: TỰ LUẬN Bài 13. Một cửa hàng bán một tấm vải. Biết rằng nếu bán $\frac{5}{8}$ tấm vải đó với giá 40 nghìn đồng một mét thì lãi được 200 nghìn đồng; số vải còn lại bán với giá 38 nghìn đồng một mét thì lãi được 90 nghìn đồng. Hỏi cả tấm vải dài bao nhiêu mét? Bài 14. Cho hình chữ nhật ABCD (như hình vẽ). M là một điểm trên cạnh CD, Nối AM và BD cắt nhau tại I. Biết diện tích SBMC = 36cm2 và bằng $\frac{9}{{16}}$ SIMD. Tính diện tích tam giác ABI. Bài 15. Lúc 6 giờ 30 phút sáng, một người đi bộ trên quãng đường từ A đến B dài 10 km gồm 3 đoạn: đoạn lên dốc đi với vận tốc 3 km/giờ, đoạn xuống dốc đi với vận tốc 6 km/giờ, và một đoạn đường bằng dài 6 km. Khi đến B, người đó quay lại A ngay theo đường cũ và về tới A lúc 11 giờ 30 phút sáng cùng ngày. Tính thời gian người đó đi trên đoạn đường bằng cả đi lẫn về.
Đáp án
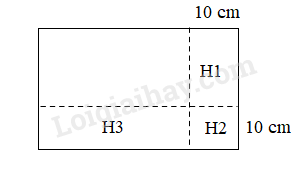
HƯỚNG DẪN GIẢI CHI TIẾT PHẦN 1: TRẮC NGHIỆM Câu 1 Tính A = 0,12 x 135 x 4 + 6,5 x 4,8 = ? Cách giải A = 0,12 x 135 x 4 + 6,5 x 4,8 = 135 x 0,48 + 6,5 x 4,8 = 13,5 x 4,8 + 6,5 x 4,8 = 4,8 x (13,5 + 6,5) = 4,8 x 20 = 96 Câu 2. Cho một hình chữ nhật có chu vi 160cm, sau khi cùng giảm chiều dài và rộng đi cùng một độ dài thì hình mới có chu vi 120cm. Vậy diện tích của phần giảm đi là bao nhiêu? Cách giải Chu vi hình chữ nhật giảm đi là 160 – 120 = 40 (cm) Độ dài mỗi cạnh giảm đi là 40 : 4 = 10 (cm)
Nửa chu vi hình chữ nhật mới là 120 : 2 = 60 (cm) Diện tích của phần giảm đi là: 10 x chiều dài mới + 10 x chiều rộng mới + 10 x 10 = 10 x (chiều dài mới + chiều rộng mới) + 100 = 10 x 60 + 100 = 700 (cm2) Đáp số: 700 cm2
Câu 3. Một đội công nhân dự định làm xong một đoạn đường trong 10 ngày. Sau khi đội đó làm được 5 ngày, người ta điều thêm một đội khác đến cùng làm nên sau 4 ngày nữa thì cả hai đội đã làm xong đoạn đường. Hỏi nếu đội thứ hai làm một mình thì phải mất bao nhiêu ngày mới làm xong cả đoạn đường đó? Cách giải Đội thứ nhất mỗi ngày làm được $1:10 = \frac{1}{{10}}$(đoạn đường) Sau 5 ngày, đội thứ nhất làm được $5 \times \frac{1}{{10}} = \frac{1}{2}$ (đoạn đường) 4 ngày 2 đội cùng làm được $1 - \frac{1}{2} = \frac{1}{2}$ (đoạn đường) Mỗi ngày hai đội cùng làm được $\frac{1}{2}:4 = \frac{1}{8}$(đoạn đường) Mỗi ngày đội thứ hai làm được $\frac{1}{8} - \frac{1}{{10}} = \frac{1}{{40}}$ (đoạn đường) Đội thứ hai làm một mình xong cả đoạn đường trong số ngày là $1:\frac{1}{{40}} = 40$ (ngày) Đáp số: 40 ngày
Câu 4. Một số tự nhiên được viết bởi 2020 chữ số 1. Hỏi phải cộng thêm vào số đó ít nhất bao nhiêu đơn vị để được một số chia hết cho 9? Cách giải Tổng các chữ số của số đó là 2020 x 1 = 2020 Mà 2 + 0 + 2 + 0 = 4 nên để số đó chia hết cho 9 thì phải cộng thêm vào số đó 5 ; 14 ; 23 ; .... đơn vị Vì số cần tìm là nhỏ nhất nên ta cộng thêm vào số đó 5 đơn vị. Đáp số: 5 đơn vị
Câu 5. Một hình lập phương có diện tích toàn phần là 150cm2. Tính thể tích của hình lập phương đó. Cách giải S toàn phần = cạnh x cạnh x 6 = 150 $ \Rightarrow $ cạnh x cạnh = 150 : 6 = 25 $ \Rightarrow $ độ dài cạnh hình lập phương bằng 5 cm Thể tích của hình lập phương là 5 x 5 x 5 = 125 (cm3) Đáp số: 125 cm3 Câu 6. Cho một hình hộp chữ nhật. Người ta tăng chiều dài của hình hộp chữ nhật 10% và giảm chiều rộng của nó đi 20% . Hỏi để thể tích hình hộp chữ nhật tăng 32% thì chiều cao của hình hộp cần tăng thêm bao nhiêu phần trăm? Cách giải Ta có V = chiều dài x chiều rộng x chiều cao 132% x V = 110% x chiều dài x 80% x chiều rộng x chiều cao mới Chiều cao mới = 132% : (110% x 80%) = 132% : 88% = 150% chiều cao ban đầu Vậy chiều cao của hình hộp cần tăng thêm 50%. Đáp số: 50%
Câu 7. Một bữa tiệc có sự tham gia của 10 cặp vợ chồng. Biết mỗi người chồng bắt tay với tất cả mọi người trừ vợ của mình và những người vợ không bắt tay nhau. Hỏi có tất cả bao nhiêu cái bắt tay? Cách giải Mỗi người chồng bắt tay với 9 người chồng còn lại + 9 người vợ $ \to $ 18 cái bắt tay 10 người chồng như vậy thì có 18 x 10 : 2 = 90 (cái bắt tay) Mỗi người vợ bắt tay với 9 người chồng $ \to $ 9 cái bắt tay Vậy 10 người vợ thì có 9 x 10 : 2 = 45 (cái bắt tay) Vậy 10 cặp vợ chồng thì có tất cả 90 + 45 = 135 (cái bắt tay) Đáp số: 135 cái bắt tay Câu 8. Năm sinh của một cầu thủ bóng đá là $\overline {19ab} $. Tính đến năm 2021, tuổi của cầu thủ này đúng bằng tổng các chữ số của năm sinh. Hỏi năm nay cầu thủ đó bao nhiêu tuổi? Cách giải Theo đề bài ta có 2021 - $\overline {19ab} $= 1 + 9 + a + b 2021 – (1900 + a x 10 + b) = 10 + a + b 2021 – 1900 – a x 10 – b = 10 + a + b 2021 – 1900 – 10 = a + a x 10 + b + b 111 = a x 11 + b x 2 Theo tính chất chẵn, lẻ thì a là số lẻ Thử a = 1 ; 3 ; 5 ; 7 hoặc 9 vào ta thấy chỉ có a = 9 thỏa mãn Khi đó b = 6. Vậy năm sinh của cầu thủ là 1996 Năm 2020, tuổi của cầu thủ là 2020 – 1996 = 24 tuổi Đáp số: 24 tuổi Câu 9. Người ta tạo ra một dãy số bằng cách viết liên tiếp các số tự nhiên khác 0 được tạo thành từ các chữ số 0 ; 2 (số lần lặp lại tùy ý) theo thứ tự tăng dần. Hỏi số 2 000 020 là số thứ bao nhiêu trong dãy số trên? Cách giải Các số trong dãy là 2 ; 20 ; 22 ; 200 ; 202 ; 220 ; 222 ; .... Xét số có 1 chữ số: có 1 số Số có 2 chữ số: có 1 x 2 số Số có 3 chữ số: có 1 x 2 x 2 = 4 số Số có 4 chữ số: có 1 x 2 x 2 x 2 = 8 số Số có 5 chữ số: có 1 x 2 x 2 x 2 x 2 = 16 số Số có 6 chữ số: có 1 x 2 x 2 x 2 x 2 x 2 = 32 số Số có 7 chữ số: 2 000 000 ; 2 000 002 ; 2 000 020 Vậy số 2 000 020 là số thứ 1 + 2 + 4 + 8 + 16 + 32 + 3 = 66 Đáp số: số thứ 66
Câu 10. Bài thi có hai phần trắc nghiệm và tự luận, mỗi câu trắc nghiệm đúng được 0,5 điểm, mỗi câu tự luận đúng được 1,0 điểm, câu sai hoặc không làm thì không được điểm. Bạn A đi thi làm được tổng cộng 30 câu và được 18,5 điểm. Hỏi bạn A làm đúng bao nhiêu câu trắc nghiệm? Cách giải Giả sử bạn A làm đúng 30 câu tự luận thì số điểm A đạt được là 30 x 1 = 30 (điểm) Khi đó số điểm tăng lên là 30 – 18,5 = 11,5 (điểm) Vì mỗi câu tự luận thay cho mỗi câu trắc nghiệm nên số điểm tăng lên mỗi câu là 0,5 điểm Vậy số câu trắc nghiệm A làm đúng là 11,5 : 0,5 = 23 (câu) Đáp số: 23 câu trắc nghiệm
Câu 11. Một cửa hàng nhập về một số hộp bánh. Cô bán bánh bày $\frac{1}{{10}}$ số hộp ở quầy để bán, còn lại cất vào kho. Sau khi bán đi 6 hộp ở quầy, cô ấy nhận thấy số hộp cất trong kho gấp 15 lần số hộp còn lại ở quầy. Hỏi lúc đầu cửa hàng nhập về bao nhiêu hộp bánh? Cách giải Nhận xét: số hộp trong kho không thay đổi Lúc đầu, số hộp ở quầy bằng $\frac{1}{9}$ số hộp trong kho Sau khi bán 6 hộp, số hộp ở quầy = $\frac{1}{{15}}$ số hộp trong kho 6 hộp ứng với $\frac{1}{9} - \frac{1}{{15}} = \frac{2}{{45}}$ (số hộp trong kho) Số hộp trong kho là $6:\frac{2}{{45}} = 135$ (hộp) Số hộp ở quầy trước khi bán là 135 : 9 = 15 (hộp) Vậy lúc đầu cửa hàng nhập về 135 + 15 = 150 (hộp) Đáp số: 150 hộp
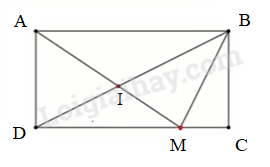
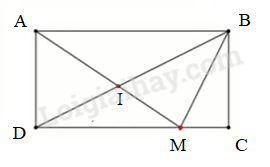
Câu 12. Một cửa hàng hoa quả có 420 kg táo và lê. Sau khi bán, người bán hàng nhận thấy: số táo đã bán bằng $\frac{1}{6}$ số lê đã bán và số táo còn lại nhiều hơn số lê còn lại 40 kg. Hỏi cửa hàng đó đã bán được bao nhiêu ki-lô-gam lê, biết rằng lúc đầu số táo bằng $\frac{3}{4}$ số lê. Cách giải: Số kg táo lúc đầu là 420 : (3 + 4) x 3 = 180 (kg) Số kg lê lúc đầu là 420 – 180 = 240 (kg) Lúc đầu số kg lê nhiều hơn số kg táo là 240 – 180 = 60 (kg) Số kg lê bán nhiều hơn số kg táo là 60 + 40 = 100 (kg) Số kg táo đã bán là 100 : (6 – 1) x 1 = 20 (kg) Số kg lê đã bán là 100 + 20 = 120 (kg) Đáp số: 120 kg lê PHẦN 2: TỰ LUẬN Bài 13. Một cửa hàng bán một tấm vải. Biết rằng nếu bán $\frac{5}{8}$ tấm vải đó với giá 40 nghìn đồng một mét thì lãi được 200 nghìn đồng; số vải còn lại bán với giá 38 nghìn đồng một mét thì lãi được 90 nghìn đồng. Hỏi cả tấm vải dài bao nhiêu mét? Cách giải Nếu bán cả tấm vải với giá 40 nghìn đồng/mét thì số tiền lãi là $200:\frac{5}{8} = 320$ (nghìn) Nếu bán cả tấm vải với giá 38 nghìn đồng/mét thì số tiền lãi là $90:(1 - \frac{5}{8}) = 240$ (nghìn) Tấm vải dài số mét là (320 – 240) : (40 – 38) = 40 (mét) Đáp số: 40 m Bài 14. Cho hình chữ nhật ABCD (như hình vẽ). M là một điểm trên cạnh CD, Nối AM và BD cắt nhau tại I. Biết diện tích SBMC = 36cm2 và bằng $\frac{9}{{16}}$ SIMD. Tính diện tích tam giác ABI.
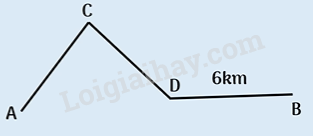
Ta có SIMD = $36:\frac{9}{{16}} = 64$ (cm2) Xét hình thang ABCD có SADM = SBDM (chung đáy DM và chiều cao bằng nhau) Mà SADM = SADI + SIMD ; SBDM = SBMI + SIMD SADI = SBMI (1) Ta có SABD = SBDC (= $\frac{1}{2}$x SABCD) SADI + SABI = SBMC + SBMI + SIMD (2) Từ (1) và (2) $ \Rightarrow $SABI = SBMC + SIMD = 36 + 64 = 100 (cm2) Đáp số: 100 cm2 Bài 15. Lúc 6 giờ 30 phút sáng, một người đi bộ trên quãng đường từ A đến B dài 10 km gồm 3 đoạn: đoạn lên dốc đi với vận tốc 3 km/giờ, đoạn xuống dốc đi với vận tốc 6 km/giờ, và một đoạn đường bằng dài 6 km. Khi đến B, người đó quay lại A ngay theo đường cũ và về tới A lúc 11 giờ 30 phút sáng cùng ngày. Tính thời gian người đó đi trên đoạn đường bằng cả đi lẫn về. Cách giải Giả sử quãng đường AB như hình vẽ:
Độ dài quãng đường dốc là AC + CD = 10 – 6 = 4 (km) Tổng thời gian lên dốc, xuống dốc cả đi và về là: $\frac{{AC}}{3} + \frac{{CD}}{6} + \frac{{CD}}{3} + \frac{{AC}}{6} = \frac{{AC + CD}}{3} + \frac{{AC + CD}}{6} = \frac{4}{3} + \frac{4}{6} = 2$ (giờ) Thời gian người đó đi trên quãng đường bằng cả đi lẫn về là 11 giờ 30 phút – 6 giờ 30 phút – 2 giờ = 3 (giờ) Đáp số: 3 giờ
|




















Danh sách bình luận