Đề thi, đề kiểm tra Toán lớp 11 - Kết nối tri thức

Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Phần trắc nghiệm (7 điểm) Câu 1: Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

Đề bài

I. Trắc nghiệm
Câu 1 :

Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

  • A
    \({\left( {{a^m}} \right)^n} = {a^{m + n}}\).
  • B
    \({\left( {{a^m}} \right)^n} = {a^{m - n}}\).
  • C
    \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
  • D
    \({\left( {{a^m}} \right)^n} = {a^{\frac{m}{n}}}\).
Câu 2 :

Chọn đáp án đúng.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:

  • A
    \({a^{ - n}} = \frac{1}{{{a^n}}}\).
  • B
    \({a^{1 - n}} = \frac{1}{{{a^n}}}\).
  • C
    \({a^{\frac{1}{n}}} = \frac{1}{{{a^n}}}\).
  • D
    Cả A, B, C đều sai.
Câu 3 :

Chọn đáp án đúng:

  • A
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[6]{{ab}}\).
  • B
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[9]{{ab}}\).
  • C
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{a + b}}\).
  • D
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).
Câu 4 :

Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).

  • A
    \({a^2}\).
  • B
    a.
  • C
    \(\frac{1}{a}\).
  • D
    \(2{a^2}\).
Câu 5 :

Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?

  • A
    \(a = \frac{3}{4}\).
  • B
    \(a = \frac{1}{2}\).
  • C
    \(a = 1\).
  • D
    \(a = \frac{3}{2}\).
Câu 6 :

Chọn đáp án đúng.

\({\log _a}b\) xác định khi và chỉ khi:

  • A
    \(a > 0\).
  • B
    \(a > 1\).
  • C
    \(a > 0,a \ne 1,b > 0\).
  • D
    \(a > 1,b > 0\).
Câu 7 :

Chọn đáp án đúng.

  • A
    \({\log _{1000}}{1000^3} = {1000^3}\).
  • B
    \({\log _{1000}}{1000^3} = \frac{1}{3}\).
  • C
    \({\log _{1000}}{1000^3} = 3\).
  • D
    \({\log _{1000}}{1000^3} = {3^{1000}}\).
Câu 8 :

Khẳng định nào sau đây đúng?

  • A
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
  • B
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
  • C
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
  • D
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\ln a\).
Câu 9 :

Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:

  • A
    81.
  • B
    \(9\).
  • C
    \(\frac{1}{{81}}\).
  • D
    \(\frac{1}{9}\).
Câu 10 :

Chọn đáp án đúng:

  • A
    \({\log _5}15 - 2{\log _5}\sqrt 3  =  - 1\).
  • B
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 1\).
  • C
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 0\).
  • D
    \({\log _5}15 - 2{\log _5}\sqrt 3  = \frac{1}{2}\).
Câu 11 :

Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    3.
Câu 12 :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:

  • A
    \(D = \left( {0; + \infty } \right)\).
  • B
    \(D = \left( { - \infty ;0} \right)\).
  • C
    \(D = \left( { - \infty ; + \infty } \right)\).
  • D
    Cả A, B, C đều sai.
Câu 13 :

Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?

  • A
    \(\left( { - 1; + \infty } \right)\).
  • B
    \(\left[ {0; + \infty } \right)\).
  • C
    \(\left[ { - 1; + \infty } \right)\).
  • D
    \(\left( {1; + \infty } \right)\).
Câu 14 :

Hàm số nào dưới đây là hàm số mũ?

  • A
    \(y = {x^{\sqrt 2 }}\).
  • B
    \(y = {x^{\log 4}}\).
  • C
    \(y = {\left( {\frac{\pi }{2}} \right)^x}\).
  • D
    \(y = {\log _2}x\).
Câu 15 :

Hàm số nào dưới đây có đồ thị như hình dưới?

  • A
    \(y = {3^x}\).
  • B
    \(y = {\left( {\frac{1}{2}} \right)^x}\).
  • C
    \(y = {\left( {\frac{1}{3}} \right)^x}\).
  • D
    \(y = {\left( {\sqrt 2 } \right)^x}\).
Câu 16 :

Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:

  • A
    \(M.m = 2\).
  • B
    \(M.m = \frac{1}{2}\)
  • C
    \(M.m = 4\).
  • D
    \(M.m = \frac{1}{4}\).
Câu 17 :

Nghiệm của phương trình \({2^x} = 9\) là:

  • A
    \(x = {\log _9}2\).
  • B
    \(x = {\log _2}9\).
  • C
    \(x = {2^{ - 9}}\)
  • D
    \(x = \frac{9}{2}\).
Câu 18 :

Nghiệm của phương trình \({2^{2x - 1}} = {2^x}\) là:

  • A
    \(x = 0\).
  • B
    \(x = 2\).
  • C
    \(x =  - 1\).
  • D
    \(x = 1\).
Câu 19 :

Phương trình \({\pi ^{x - 3}} = \frac{1}{\pi }\) có nghiệm là:

  • A
    \(x = 0\).
  • B
    \(x = 2\).
  • C
    \(x =  - 1\).
  • D
    \(x = 1\).
Câu 20 :

Nghiệm của phương trình \({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}}\) là:

  • A
    \(x = \frac{{ - 1}}{4}\).
  • B
    \(x = \frac{1}{4}\).
  • C
    \(x = \frac{{ - 1}}{8}\).
  • D
    \(x = \frac{1}{8}\).
Câu 21 :

Tập nghiệm của bất phương trình \({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1\) là:

  • A
    \(S = \left( {3;\frac{{11}}{3}} \right)\).
  • B
    \(S = \left( {3;\frac{{11}}{3}} \right]\).
  • C
    \(S = \left[ {3;\frac{{11}}{3}} \right]\).
  • D
    \(S = \left[ {3;\frac{{11}}{3}} \right)\).
Câu 22 :

Phương trình \({\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)\) có bao nhiêu nghiệm?

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    Vô số.
Câu 23 :

Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}}\) là:

  • A
    \(S = \left( { - 2; + \infty } \right)\).
  • B
    \(S = \left( {2; + \infty } \right)\).
  • C
    \(S = \left( { - \infty ; - 2} \right)\).
  • D
    \(S = \left( { - \infty ;2} \right)\).
Câu 24 :

Góc giữa hai đường thẳng a và b có thể bằng:

  • A
    1800.
  • B
    1500.
  • C
    900.
  • D
    Cả A, B, C đều sai.
Câu 25 :

Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đúng?

  • A
    a và b cắt nhau.
  • B
    a và b chéo nhau.
  • C
    a và b cùng nằm trên một mặt phẳng.
  • D
    Góc giữa a và b bằng \({90^0}\).
Câu 26 :

Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).
Câu 27 :

Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Khi đó, góc giữa hai đường thẳng AC và MN bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).
Câu 28 :

Có bao nhiêu mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước?

  • A
    Vô số.
  • B
    1.
  • C
    2.
  • D
    3.
Câu 29 :

Chọn đáp án đúng:

  • A
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
  • B
    Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
  • C
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
  • D
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
Câu 30 :

Chọn đáp án đúng.

  • A
    Có hai đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • B
    Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • C
    Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • D
    Có ba đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Câu 31 :

Cho đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P. Góc giữa hai đường thẳng d và d’ bằng bao nhiêu độ?

  • A
    \({30^0}\).
  • B
    \({45^0}\).
  • C
    \({60^0}\).
  • D
    \({90^0}\).
Câu 32 :

Cho hình chóp S. ABCD có ABCD là hình chữ nhật, SA vuông góc với đáy. Đường thẳng BC vuông góc với mặt phẳng nào?

  • A
    (SAD).
  • B
    (SCD).
  • C
    (SAC).
  • D
    (SAB).
Câu 33 :

Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng.

  • A
    \(BC \bot AB\).
  • B
    \(BC \bot AH\).
  • C
    \(BC \bot SC\).
  • D
    Cả A, B, C đều sai.
Câu 34 :

Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’A và D’B’ bằng:

  • A
    \({30^0}\).
  • B
    \({60^0}\).
  • C
    \({90^0}\).
  • D
    \({45^0}\).
Câu 35 :

Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.

  • A
    \(\left( {AB,SD} \right) = {90^0}\).
  • B
    \(\left( {AB,SD} \right) = {85^0}\).
  • C
    \(\left( {AB,SD} \right) = {70^0}\).
  • D
    \(\left( {AB,SD} \right) = {75^0}\).
II. Tự luận
Câu 1 :

Cho hàm số: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\).

a) Với \(m = \frac{1}{3}\), hãy tìm tập xác định của hàm số trên.

b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định là \(\mathbb{R}\).
Câu 2 :

Cho hình chóp S. ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC và SD. Chứng minh rằng:

a) \(SC \bot \left( {AHK} \right)\).

b) \(HK \bot \left( {SAC} \right)\) và \(HK \bot AI\).
Câu 3 :

Có bao nhiêu số tự nhiên x thỏa mãn bất phương trình \({\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}\)?

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?

  • A
    \({\left( {{a^m}} \right)^n} = {a^{m + n}}\).
  • B
    \({\left( {{a^m}} \right)^n} = {a^{m - n}}\).
  • C
    \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
  • D
    \({\left( {{a^m}} \right)^n} = {a^{\frac{m}{n}}}\).

Đáp án : C

Phương pháp giải :

Với a là số thực dương và m, n là hai số thực tùy ý thì \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).

Lời giải chi tiết :

Với a là số thực dương và m, n là hai số thực tùy ý thì \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).

Câu 2 :

Chọn đáp án đúng.

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:

  • A
    \({a^{ - n}} = \frac{1}{{{a^n}}}\).
  • B
    \({a^{1 - n}} = \frac{1}{{{a^n}}}\).
  • C
    \({a^{\frac{1}{n}}} = \frac{1}{{{a^n}}}\).
  • D
    Cả A, B, C đều sai.

Đáp án : A

Phương pháp giải :

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì \({a^{ - n}} = \frac{1}{{{a^n}}}\).

Lời giải chi tiết :

Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì \({a^{ - n}} = \frac{1}{{{a^n}}}\).

Câu 3 :

Chọn đáp án đúng:

  • A
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[6]{{ab}}\).
  • B
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[9]{{ab}}\).
  • C
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{a + b}}\).
  • D
    \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).

Đáp án : D

Phương pháp giải :

\(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\) (với các biểu thức đều có nghĩa).

Lời giải chi tiết :

Ta có: \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).

Câu 4 :

Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).

  • A
    \({a^2}\).
  • B
    a.
  • C
    \(\frac{1}{a}\).
  • D
    \(2{a^2}\).

Đáp án : B

Phương pháp giải :

\({a^m}.{a^n} = {a^{m + n}};{\left( {{a^m}} \right)^n} = {a^{mn}},{a^m}:{a^n} = {a^{m - n}}\) (a khác 0).

Lời giải chi tiết :

\(P = \frac{{{a^{\sqrt 5  + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}} = \frac{{{a^{\sqrt 5  + 1 + 7 - \sqrt 5 }}}}{{{a^{\left( {3 + \sqrt 2 } \right)\left( {3 - \sqrt 2 } \right)}}}} = \frac{{{a^8}}}{{{a^7}}} = a\)

Câu 5 :

Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?

  • A
    \(a = \frac{3}{4}\).
  • B
    \(a = \frac{1}{2}\).
  • C
    \(a = 1\).
  • D
    \(a = \frac{3}{2}\).

Đáp án : D

Phương pháp giải :

Nếu \(a > 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha  > \beta \)

Nếu \(0 < a < 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha  < \beta \)

Lời giải chi tiết :

Ta có: \(\frac{1}{{{a^{ - 3}}}} = {a^3} = {a^{\sqrt 9 }}\) nên \({a^{\sqrt 8 }} < {a^{\sqrt 9 }}\)

Vì \(\sqrt 8  < \sqrt 9 \), mà \({a^{\sqrt 8 }} < {a^{\sqrt 9 }}\) nên \(a > 1\). Do đó, \(a = \frac{3}{2}\) thỏa mãn yêu cầu bài toán.

Câu 6 :

Chọn đáp án đúng.

\({\log _a}b\) xác định khi và chỉ khi:

  • A
    \(a > 0\).
  • B
    \(a > 1\).
  • C
    \(a > 0,a \ne 1,b > 0\).
  • D
    \(a > 1,b > 0\).

Đáp án : C

Phương pháp giải :

\({\log _a}b\) xác định khi và chỉ khi \(a > 0,a \ne 1,b > 0\).

Lời giải chi tiết :

\({\log _a}b\) xác định khi và chỉ khi \(a > 0,a \ne 1,b > 0\).

Câu 7 :

Chọn đáp án đúng.

  • A
    \({\log _{1000}}{1000^3} = {1000^3}\).
  • B
    \({\log _{1000}}{1000^3} = \frac{1}{3}\).
  • C
    \({\log _{1000}}{1000^3} = 3\).
  • D
    \({\log _{1000}}{1000^3} = {3^{1000}}\).

Đáp án : C

Phương pháp giải :

Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{a^b} = b\).

Lời giải chi tiết :

\({\log _{1000}}{1000^3} = 3\)

Câu 8 :

Khẳng định nào sau đây đúng?

  • A
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
  • B
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
  • C
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
  • D
    Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\ln a\).

Đáp án : B

Phương pháp giải :

Lôgarit cơ số 10 của số thực dương b được gọi là lôgarit thập phân của b và kí hiệu logb hay lg b.

Lôgarit cơ số e của số thực dương b được gọi là lôgarit tự nhiên của b và kí hiệu ln b.

Lời giải chi tiết :

Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).

Câu 9 :

Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:

  • A
    81.
  • B
    \(9\).
  • C
    \(\frac{1}{{81}}\).
  • D
    \(\frac{1}{9}\).

Đáp án : A

Phương pháp giải :

Với a, b là số thực dương và \(a \ne 1\) thì \({a^{{{\log }_a}b}} = b,{\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b;{\log _a}{b^\alpha } = \alpha {\log _a}b\).

Lời giải chi tiết :

\({4^{{{\log }_{\sqrt 2 }}3}} = {2^{2{{\log }_{{2^{\frac{1}{2}}}}}3}} = {2^{4{{\log }_2}3}} = {2^{{{\log }_2}{3^4}}} = 81\)

Câu 10 :

Chọn đáp án đúng:

  • A
    \({\log _5}15 - 2{\log _5}\sqrt 3  =  - 1\).
  • B
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 1\).
  • C
    \({\log _5}15 - 2{\log _5}\sqrt 3  = 0\).
  • D
    \({\log _5}15 - 2{\log _5}\sqrt 3  = \frac{1}{2}\).

Đáp án : B

Phương pháp giải :

Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{b^\alpha } = \alpha {\log _a}b,\log {\,_a}a = 1\)

Với a là số thực dương, \(a \ne 1\), \(M > 0,N > 0\) thì \({\log _a}\frac{M}{N} = {\log _a}M - {\log _a}N\).

Lời giải chi tiết :

\({\log _5}15 - 2{\log _5}\sqrt 3  = {\log _5}15 - {\log _5}3 = {\log _5}\frac{{15}}{3} = {\log _5}5 = 1\)

Câu 11 :

Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    3.

Đáp án : B

Phương pháp giải :

Đồ thị hàm số hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng 1.

Lời giải chi tiết :

Đồ thị hàm số hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng 1.

Câu 12 :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:

  • A
    \(D = \left( {0; + \infty } \right)\).
  • B
    \(D = \left( { - \infty ;0} \right)\).
  • C
    \(D = \left( { - \infty ; + \infty } \right)\).
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(D = \left( { - \infty ; + \infty } \right)\).

Lời giải chi tiết :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(D = \left( { - \infty ; + \infty } \right)\).

Câu 13 :

Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?

  • A
    \(\left( { - 1; + \infty } \right)\).
  • B
    \(\left[ {0; + \infty } \right)\).
  • C
    \(\left[ { - 1; + \infty } \right)\).
  • D
    \(\left( {1; + \infty } \right)\).

Đáp án : D

Phương pháp giải :

Nếu \(a > 1\) thì hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {0; + \infty } \right)\).

Lời giải chi tiết :

Vì \(2 > 1\) nên hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {0; + \infty } \right)\). Do đó, hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {1; + \infty } \right)\)

Câu 14 :

Hàm số nào dưới đây là hàm số mũ?

  • A
    \(y = {x^{\sqrt 2 }}\).
  • B
    \(y = {x^{\log 4}}\).
  • C
    \(y = {\left( {\frac{\pi }{2}} \right)^x}\).
  • D
    \(y = {\log _2}x\).

Đáp án : C

Phương pháp giải :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.

Lời giải chi tiết :

Hàm số \(y = {\left( {\frac{\pi }{2}} \right)^x}\) được gọi là hàm số mũ.

Câu 15 :

Hàm số nào dưới đây có đồ thị như hình dưới?

  • A
    \(y = {3^x}\).
  • B
    \(y = {\left( {\frac{1}{2}} \right)^x}\).
  • C
    \(y = {\left( {\frac{1}{3}} \right)^x}\).
  • D
    \(y = {\left( {\sqrt 2 } \right)^x}\).

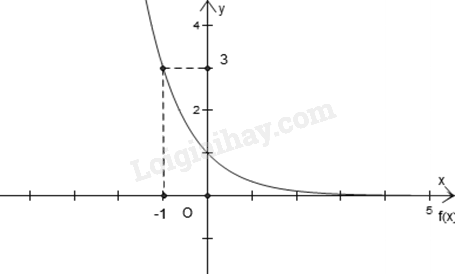
Đáp án : C

Phương pháp giải :

Xét xem đồ thị hàm số nào đi qua điểm \(\left( { - 1;3} \right)\) và (0;1) thì đó là đồ thị hàm số cần tìm.

Lời giải chi tiết :

Ta thấy đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) đi qua điểm \(\left( { - 1;3} \right)\) và (0;1) nên hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) là hàm số cần tìm.

Câu 16 :

Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:

  • A
    \(M.m = 2\).
  • B
    \(M.m = \frac{1}{2}\)
  • C
    \(M.m = 4\).
  • D
    \(M.m = \frac{1}{4}\).

Đáp án : A

Phương pháp giải :

Cho hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\):

+ Nếu \(a > 1\) thì hàm số đồng biến trên \(\mathbb{R}\).

+ Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \(\mathbb{R}\).

Lời giải chi tiết :

Vì \(2 > 1\) nên hàm số \(f\left( x \right) = {2^x}\) đồng biến trên \(\mathbb{R}\).

Do đó, \(\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right) = {2^3} = 8;\mathop {\min }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( { - 2} \right) = {2^{ - 2}} = \frac{1}{4}\)

Suy ra: \(M = 8,m = \frac{1}{4} \Rightarrow Mm = 8.\frac{1}{4} = 2\).

Câu 17 :

Nghiệm của phương trình \({2^x} = 9\) là:

  • A
    \(x = {\log _9}2\).
  • B
    \(x = {\log _2}9\).
  • C
    \(x = {2^{ - 9}}\)
  • D
    \(x = \frac{9}{2}\).

Đáp án : B

Phương pháp giải :

Cho phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\):

+ Nếu \(b \le 0\) thì phương trình vô nghiệm.

+ Nếu \(b > 0\) thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).

Lời giải chi tiết :

\({2^x} = 9 \Leftrightarrow x = {\log _2}9\)

Vậy phương trình có nghiệm là \(x = {\log _2}9\).

Câu 18 :

Nghiệm của phương trình \({2^{2x - 1}} = {2^x}\) là:

  • A
    \(x = 0\).
  • B
    \(x = 2\).
  • C
    \(x =  - 1\).
  • D
    \(x = 1\).

Đáp án : D

Phương pháp giải :

\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)

Lời giải chi tiết :

\({2^{2x - 1}} = {2^x} \Leftrightarrow 2x - 1 = x \Leftrightarrow x = 1\)

Vậy phương trình đã cho có nghiệm \(x = 1\)

Câu 19 :

Phương trình \({\pi ^{x - 3}} = \frac{1}{\pi }\) có nghiệm là:

  • A
    \(x = 0\).
  • B
    \(x = 2\).
  • C
    \(x =  - 1\).
  • D
    \(x = 1\).

Đáp án : B

Phương pháp giải :

\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)

Lời giải chi tiết :

\({\pi ^{x - 3}} = \frac{1}{\pi } \Leftrightarrow {\pi ^{x - 3}} = {\pi ^{ - 1}} \Leftrightarrow x - 3 =  - 1 \Leftrightarrow x = 2\)

Vậy phương trình có nghiệm \(x = 2\).

Câu 20 :

Nghiệm của phương trình \({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}}\) là:

  • A
    \(x = \frac{{ - 1}}{4}\).
  • B
    \(x = \frac{1}{4}\).
  • C
    \(x = \frac{{ - 1}}{8}\).
  • D
    \(x = \frac{1}{8}\).

Đáp án : A

Phương pháp giải :

\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)

Lời giải chi tiết :

\({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}} \Leftrightarrow {4^{ - 2\left( {x + 1} \right)}} = {4^{3.2x}} \Leftrightarrow  - 2x - 2 = 6x \Leftrightarrow 8x =  - 2 \Leftrightarrow x = \frac{{ - 1}}{4}\)

Câu 21 :

Tập nghiệm của bất phương trình \({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1\) là:

  • A
    \(S = \left( {3;\frac{{11}}{3}} \right)\).
  • B
    \(S = \left( {3;\frac{{11}}{3}} \right]\).
  • C
    \(S = \left[ {3;\frac{{11}}{3}} \right]\).
  • D
    \(S = \left[ {3;\frac{{11}}{3}} \right)\).

Đáp án : B

Phương pháp giải :

Nếu \(0 < a < 1\) thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) \le v\left( x \right)\end{array} \right.\).

Lời giải chi tiết :

\({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1 \Leftrightarrow {\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge {\log _{\frac{2}{3}}}\frac{2}{3} \Leftrightarrow \left\{ \begin{array}{l}x - 3 > 0\\x - 3 \le \frac{2}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 3\\x \le \frac{{11}}{3}\end{array} \right.\)

Do đó, tập nghiệm của bất phương trình là: \(S = \left( {3;\frac{{11}}{3}} \right]\).

Câu 22 :

Phương trình \({\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)\) có bao nhiêu nghiệm?

  • A
    0.
  • B
    1.
  • C
    2.
  • D
    Vô số.

Đáp án : B

Phương pháp giải :

Với \(a > 0,a \ne 1\) thì \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\))

Lời giải chi tiết :

Điều kiện: \(x > 0\)

\({\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right) \Leftrightarrow {\log _3}x\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)\)

\( \Leftrightarrow {x^2} + x = 5x + 12 \Leftrightarrow {x^2} - 4x - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 2\left( L \right)\\x = 6\left( {TM} \right)\end{array} \right.\)

Vậy phương trình đã cho có một nghiệm là \(x = 6\)

Câu 23 :

Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}}\) là:

  • A
    \(S = \left( { - 2; + \infty } \right)\).
  • B
    \(S = \left( {2; + \infty } \right)\).
  • C
    \(S = \left( { - \infty ; - 2} \right)\).
  • D
    \(S = \left( { - \infty ;2} \right)\).

Đáp án : D

Phương pháp giải :

Với \(a > 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)\)

Lời giải chi tiết :

\({\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}} \Leftrightarrow {5^{\frac{{ - 2x}}{2}}} < {5^{2\left( {1 - x} \right)}} \Leftrightarrow  - x < 2 - 2x\left( {do\;5 > 1} \right) \Leftrightarrow x < 2\)

Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left( { - \infty ;2} \right)\).

Câu 24 :

Góc giữa hai đường thẳng a và b có thể bằng:

  • A
    1800.
  • B
    1500.
  • C
    900.
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Góc giữa hai đường thẳng có số đo không vượt quá 900.

Lời giải chi tiết :

Vì góc giữa hai đường thẳng có số đo không vượt quá 900 nên góc giữa hai đường thẳng có thể bằng 900.

Câu 25 :

Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đúng?

  • A
    a và b cắt nhau.
  • B
    a và b chéo nhau.
  • C
    a và b cùng nằm trên một mặt phẳng.
  • D
    Góc giữa a và b bằng \({90^0}\).

Đáp án : D

Phương pháp giải :

Hai đường thẳng vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).

Lời giải chi tiết :

Trong không gian cho hai đường thẳng a và b vuông góc với nhau thì góc giữa chúng bằng \({90^0}\).

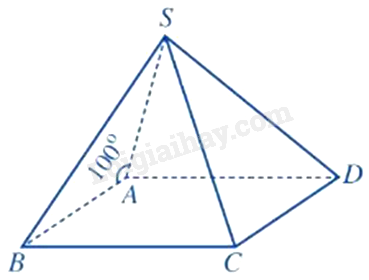
Câu 26 :

Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).

Đáp án : C

Phương pháp giải :

+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).

+ Góc giữa hai đường thẳng không vượt quá \({90^0}\).

Lời giải chi tiết :

Vì ABCD là hình bình hành nên \(AB//CD\)

Do đó, \(\left( {SA,CD} \right) = \left( {SA,AB} \right) = {180^0} - \widehat {SAB} = {80^0}\)

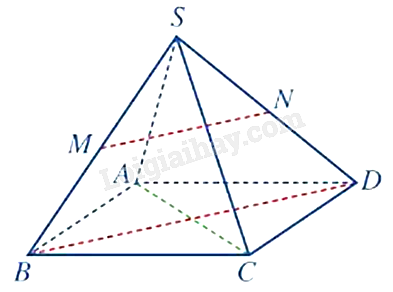
Câu 27 :

Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Khi đó, góc giữa hai đường thẳng AC và MN bằng bao nhiêu độ?

  • A
    \({100^0}\).
  • B
    \({90^0}\).
  • C
    \({80^0}\).
  • D
    \({70^0}\).

Đáp án : B

Phương pháp giải :

Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.

Lời giải chi tiết :

Vì M, N lần lượt là trung điểm của các cạnh SB và SD nên MN là đường trung bình của tam giác SBD, do đó, MN//BD.

Vì ABCD là hình thoi nên \(AC \bot BD\)

Vì \(AC \bot BD\), MN//BD nên \(AC \bot MN \Rightarrow \left( {AC,MN} \right) = {90^0}\).

Câu 28 :

Có bao nhiêu mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước?

  • A
    Vô số.
  • B
    1.
  • C
    2.
  • D
    3.

Đáp án : B

Phương pháp giải :

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Lời giải chi tiết :

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Câu 29 :

Chọn đáp án đúng:

  • A
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
  • B
    Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
  • C
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
  • D
    Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.

Đáp án : A

Phương pháp giải :

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Lời giải chi tiết :

Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Câu 30 :

Chọn đáp án đúng.

  • A
    Có hai đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • B
    Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • C
    Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
  • D
    Có ba đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Đáp án : C

Phương pháp giải :

Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Lời giải chi tiết :

Có duy nhất một đường thẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Câu 31 :

Cho đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P. Góc giữa hai đường thẳng d và d’ bằng bao nhiêu độ?

  • A
    \({30^0}\).
  • B
    \({45^0}\).
  • C
    \({60^0}\).
  • D
    \({90^0}\).

Đáp án : D

Phương pháp giải :

Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P nên \(d \bot d' \Rightarrow \left( {d,d'} \right) = {90^0}\)

Câu 32 :

Cho hình chóp S. ABCD có ABCD là hình chữ nhật, SA vuông góc với đáy. Đường thẳng BC vuông góc với mặt phẳng nào?

  • A
    (SAD).
  • B
    (SCD).
  • C
    (SAC).
  • D
    (SAB).

Đáp án : D

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)

Mà ABCD là hình chữ nhật nên \(BC \bot AB\)

Ta có: \(SA \bot BC,BC \bot AB,\) AB và SA cắt nhau tại A và nằm trong mặt phẳng (SAB).

Do đó, \(BC \bot \left( {SAB} \right)\)

Câu 33 :

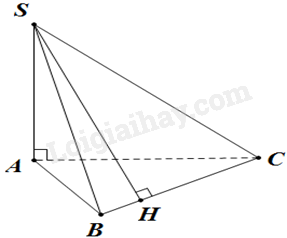
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng.

  • A
    \(BC \bot AB\).
  • B
    \(BC \bot AH\).
  • C
    \(BC \bot SC\).
  • D
    Cả A, B, C đều sai.

Đáp án : B

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\), mà \(BC \bot SH\) và SA và SH cắt nhau tại S và nằm trong mặt phẳng (SAH) nên \(BC \bot \left( {SAH} \right)\).

Lại có: \(AH \subset \left( {SAH} \right)\) nên \(BC \bot AH\).

Câu 34 :

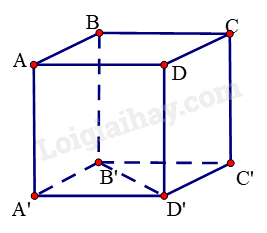
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’A và D’B’ bằng:

  • A
    \({30^0}\).
  • B
    \({60^0}\).
  • C
    \({90^0}\).
  • D
    \({45^0}\).

Đáp án : C

Phương pháp giải :

Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì ABCD.A’B’C’D’ là hình lập phương nên \(AA' \bot \left( {A'B'C'D'} \right)\), mà \(B'D' \subset \left( {A'B'C'D'} \right)\) nên \(AA' \bot B'D'\). Do đó, góc giữa hai đường thẳng A’A và D’B’ bằng \({90^0}\).

Câu 35 :

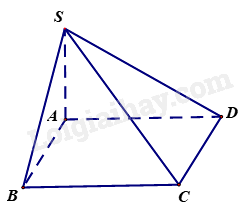
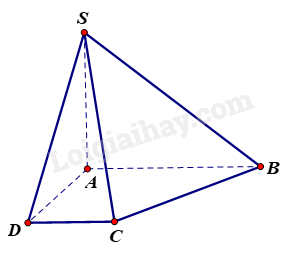
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.

  • A
    \(\left( {AB,SD} \right) = {90^0}\).
  • B
    \(\left( {AB,SD} \right) = {85^0}\).
  • C
    \(\left( {AB,SD} \right) = {70^0}\).
  • D
    \(\left( {AB,SD} \right) = {75^0}\).

Đáp án : A

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(SA \bot \left( {ABCD} \right),AB \subset \left( {ABCD} \right) \Rightarrow SA \bot AB\).

Vì ABCD là hình thang vuông tại A nên \(AB \bot AD\).

Ta có: \(AB \bot AD\), \(SA \bot AB\) và SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD)

Do đó, \(AB \bot \left( {SAD} \right) \Rightarrow AB \bot SD\). Suy ra, \(\left( {AB,SD} \right) = {90^0}\).

II. Tự luận
Câu 1 :

Cho hàm số: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\).

a) Với \(m = \frac{1}{3}\), hãy tìm tập xác định của hàm số trên.

b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định là \(\mathbb{R}\).
Phương pháp giải :

+ Hàm số có dạng \(y = \frac{1}{{\sqrt {u\left( x \right)} }}\) xác định khi \(u\left( x \right) > 0\).

+ Hàm \(y = {\log _a}u\left( x \right)\left( {a > 0,a \ne 1} \right)\) xác định khi \(u\left( x \right) > 0\).

Lời giải chi tiết :

a) Với \(m = \frac{1}{3}\) ta có: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}\).

Hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}\) xác định khi \({\log _3}\left( {{x^2} - 2x + 1} \right) > 0 \Leftrightarrow {x^2} - 2x + 1 > 1 \Leftrightarrow {x^2} - 2x > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < 0\end{array} \right.\)

Vậy với \(m = \frac{1}{3}\) thì tập xác định của hàm số là: \(D = \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\).

b) Hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\) có tập xác định là \(\mathbb{R}\) khi và chỉ khi \({\log _3}\left( {{x^2} - 2x + 3m} \right) > 0\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow {x^2} - 2x + 3m > 1\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow {x^2} - 2x + 3m - 1 > 0\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow {\left( { - 1} \right)^2} - 3m + 1 < 0 \Leftrightarrow m > \frac{2}{3}\)

Vậy với \(m > \frac{2}{3}\) thì hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\) có tập xác định là \(\mathbb{R}\).

Câu 2 :

Cho hình chóp S. ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC và SD. Chứng minh rằng:

a) \(SC \bot \left( {AHK} \right)\).

b) \(HK \bot \left( {SAC} \right)\) và \(HK \bot AI\).
Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

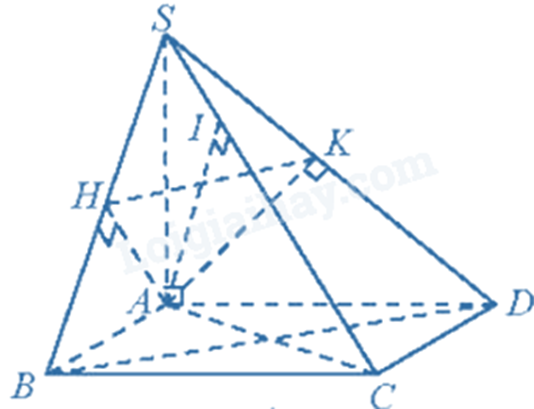
a) Vì \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\)

Vì ABCD là hình vuông nên \(DC \bot AD\).

Mà SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD). Do đó, \(DC \bot \left( {SAD} \right)\)

Lại có: \(AK \subset \left( {SAD} \right) \Rightarrow DC \bot AK\). Mặt khác, \(AK \bot SD \Rightarrow AK \bot \left( {SDC} \right) \Rightarrow AK \bot SC\)

Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)

Vì ABCD là hình vuông nên \(BC \bot AB\).

Mà SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB). Do đó, \(BC \bot \left( {SAB} \right)\)

Lại có: \(AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH\). Mặt khác, \(AH \bot SB \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)

Ta có: \(AK \bot SC\), \(AH \bot SC\) và AK và AH cắt nhau tại A nằm trong mặt phẳng (AHK) nên \(SC \bot \left( {AHK} \right)\).

b) Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot AB\\SA \bot AD\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat {SAB} = {90^0}\\\widehat {SAD} = {90^0}\end{array} \right.\)

Tam giác SAB và tam giác SAD có: SA là cạnh chung, \(\widehat {SAB} = \widehat {SAD} = {90^0}\), \(AB = AD\).

Do đó, \(\Delta SAB = \Delta SAD\left( {c.g.c} \right) \Rightarrow SB = SD\), \(SH = SK\).

Suy ra: \(\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}}\). Do đó, HK//BD (1)

Vì ABCD là hình vuông nên \(AC \bot BD\).

Vì \(SA \bot \left( {ABCD} \right),DB \subset \left( {ABCD} \right) \Rightarrow SA \bot DB\)

Mà SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên \(DB \bot \left( {SAC} \right)\) (2)

Từ (1) và (2) ta có: \(HK \bot \left( {SAC} \right)\). Mà \(AI \subset \left( {SAC} \right)\), suy ra \(HK \bot AI\).

Câu 3 :

Có bao nhiêu số tự nhiên x thỏa mãn bất phương trình \({\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}\)?
Phương pháp giải :

Nếu \(a > 1\) thì \({\log _a}u\left( x \right) < {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.\).

Lời giải chi tiết :

TXĐ: \(D = \left( { - \infty ; - 4} \right) \cup \left( {4; + \infty } \right)\).

Ta có: \({\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}\)

\(\begin{array}{l} \Leftrightarrow {\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{{x^2} - 16}}{{27}}\\ \Leftrightarrow {\rm{lo}}{{\rm{g}}_3}7.\left[ {{\rm{lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) - 3} \right] < {\rm{lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) - 3{\rm{lo}}{{\rm{g}}_7}3\\ \Leftrightarrow \left( {{\rm{lo}}{{\rm{g}}_3}7 - 1} \right){\rm{.lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) < 3{\rm{lo}}{{\rm{g}}_3}7 - 3{\rm{lo}}{{\rm{g}}_7}3\\ \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 - {{\log }_7}3} \right)}}{{{{\log }_3}7 - 1}}\end{array}\)

\( \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 - \frac{1}{{{{\log }_3}7}}} \right)}}{{{{\log }_3}7 - 1}}\)\( \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 + 1} \right)}}{{{{\log }_3}7}}\)

\(\begin{array}{l} \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < 3\left( {1 + {{\log }_7}3} \right)\\ \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < {\log _7}{21^3}\end{array}\)

\( \Leftrightarrow {x^2} - 16 < {21^3} \Leftrightarrow  - \sqrt {9277}  < x < \sqrt {9277} \)

Kết hợp với điều kiện xác định ta có: \(\left[ \begin{array}{l} - \sqrt {9277}  < x <  - 4\\4 < x < \sqrt {9277} \end{array} \right.\)

Vì x là số tự nhiên nên \(x \in \left\{ {5;6;7;...;96} \right\}\).

Bài liên quan
close