Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 1Tải về Phần trắc nghiệm (4 điểm) Câu 1: Góc lượng giác có số đo (alpha ) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau: Quảng cáo
Đề bài Phần trắc nghiệm (4 điểm) Câu 1: Góc lượng giác có số đo \(\alpha \) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau:
Câu 2: Biết \(\tan x = \frac{1}{2}\), giá trị của biểu thức \(M = \frac{{2{{\sin }^2}x + 3\sin x.\cos x - 4{{\cos }^2}x}}{{5{{\cos }^2}x - {{\sin }^2}x}}\) bằng:
Câu 3: Mệnh đề nào sau đây đúng? A. \(\tan \left( {x - y} \right) = \frac{{\tan x + \tan y}}{{\tan x\tan y}}\). B. \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 + \tan x\tan y}}\). C. \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 - \tan x\tan y}}\). D. \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{\tan x\tan y}}\). Câu 4: Công thức nào sau đây là sai? A. \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\). B. \(\cos a - \cos b = - 2\sin \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}\). C. \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\). D. \(\sin a - \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\). Câu 5: Cho các hàm số: \(y = \cos x\), \(y = \tan x\), \(y = \cot x\). Có bao nhiêu hàm số tuần hoàn với chu kỳ \(T = \pi \).
Câu 6: Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \cos 2x + \cos x.\) Khi đó \(M + m\)bằng bao nhiêu?
Câu 7: Nghiệm của phương trình \(\cos \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) là:
Câu 8: Số nghiệm của phương trình \(\cos x = \frac{1}{2}\) thuộc đoạn \(\left[ { - 2\pi ;2\pi } \right]\) là:
Câu 9: Cho dãy số có các số hạng đầu là:\(5;10;15;20;25;...\) Số hạng tổng quát của dãy số này là:
Câu 10: Cho dãy số \(SC\), biết \(AD\). Ba số hạng đầu tiên của dãy số là:
Câu 11: Trong các dãy số sau, dãy số nào là một cấp số cộng?
Câu 12: Xác định số hàng đầu \({u_1}\) và công sai \(d\) của cấp số cộng \(\left( {{u_n}} \right)\) có \({u_9} = 5{u_2}\) và \({u_{13}} = 2{u_6} + 5\).
Câu 13: Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa \(\left\{ \begin{array}{l}{u_2} - {u_3} + {u_5} = 10\\{u_4} + {u_6} = 26\end{array} \right.\). Tính \(S = {u_1} + {u_4} + {u_7} + ... + {u_{2011}}\)
Câu 14: Dãy số nào sau đây không phải là cấp số nhân?
Câu 15: Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \(\left\{ \begin{array}{l}{u_4} - {u_2} = 54\\{u_5} - {u_3} = 108\end{array} \right.\). Tìm số hạng đầu \({u_1}\) và công bội \(q\) của cấp số nhân trên.
Câu 16: Giá trị của tổng \(4 + 44 + 444 + ... + 44...4\) bằng:
Câu 17: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm \([20;40)\) là:
Câu 18: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng): Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng): Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng): Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
Phần tự luận (6 điểm) Bài 1. ( 1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = 4{\cos ^2}x - 4\cos x + 3\) với \(x \in \left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\). Bài 2. ( 1.5 điểm) a) Giải phương trình \(\sin \left( {\frac{x}{2} - \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{4}\) b) Tìm nghiệm thuộc khoảng \(\left( { - \frac{\pi }{4};2\pi } \right)\) của phương trình \(\sin \left( {\frac{\pi }{6} + 2x} \right) = - 1\). c) Giải phương trình sau: \(\cos \,x + \cos \,2x + \cos \,3x = 0\). Bài 3. ( 2 điểm) a) Cho cấp số cộng \(\left( {{u_n}} \right)\)có \({u_1} = - 2\) và \(d = 3\). Biết \({S_n} = 6095374\), tìm \(n\). b) Tìm số hạng đầu tiên và công bội của cấp số nhân sau, biết rằng: \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\). Bài 4. ( 1,5 điểm) Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên.
a) Tính trung vị của mẫu số liệu ghép nhóm này. b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này. -------- Hết -------- Lời giải chi tiết Phần trắc nghiệm (4 điểm)
Câu 1: Góc lượng giác có số đo \(\alpha \) (rad) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau:
Phương pháp - Hai góc lượng giác có cùng tia đầu và tia cuối hơn kém nhau bội nguyên lần của \(2\pi \) hoặc \({360^o}\). - Chú ý: Góc \(\alpha \) đang ở đơn vị radian Lời giải Góc lượng giác có số đo \(\alpha \) thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau: \(\alpha + k2\pi \). Đáp án C Câu 2: Biết \(\tan x = \frac{1}{2}\), giá trị của biểu thức \(M = \frac{{2{{\sin }^2}x + 3\sin x.\cos x - 4{{\cos }^2}x}}{{5{{\cos }^2}x - {{\sin }^2}x}}\) bằng:
Phương pháp B1: Từ giả thiết \(\tan x = \frac{1}{2} \Rightarrow \cos x = 2\sin x\). B2: Thay \(\cos x = 2\sin x\) vào biểu thức M sau đó rút gọn. Lời giải Ta có: \(\tan x = \frac{1}{2} \Leftrightarrow \frac{{\sin x}}{{\cos x}} = \frac{1}{2} \Leftrightarrow \cos x = 2\sin x\). Khi đó \(M = \frac{{2{{\sin }^2}x + 3\sin x.2\sin x - 4.{{\left( {2\sin x} \right)}^2}}}{{5.{{\left( {2\sin x} \right)}^2} - {{\sin }^2}x}} = \frac{{ - 8{{\sin }^2}x}}{{19{{\sin }^2}x}} = - \frac{8}{{19}}\). Đáp án D Câu 3: Mệnh đề nào sau đây đúng? A. \(\tan \left( {x - y} \right) = \frac{{\tan x + \tan y}}{{\tan x\tan y}}\). B. \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 + \tan x\tan y}}\). C. \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 - \tan x\tan y}}\). D. \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{\tan x\tan y}}\) Phương pháp Sử dụng công thức cộng. Lời giải Ta có: \(\tan \left( {x - y} \right) = \frac{{\tan x - \tan y}}{{1 + \tan x\tan y}}\). Đáp án B Câu 4: Công thức nào sau đây là sai? A. \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\). B. \(\cos a - \cos b = - 2\sin \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}\). C. \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\). D. \(\sin a - \sin b = 2\sin \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\). Phương pháp Áp dụng công thức biến đổi tổng thành tích. Lời giải Ta có: \(\sin a - \sin b = 2\cos \frac{{a + b}}{2}.\sin \frac{{a - b}}{2}\). Đáp án D Câu 5: Cho các hàm số: \(y = \cos x\), \(y = \tan x\), \(y = \cot x\). Có bao nhiêu hàm số tuần hoàn với chu kỳ \(T = \pi \).
Phương pháp Hàm số \(y = \sin x,y = \cos x\) tuần hoàn với chu kỳ \(T = 2\pi \) Hàm số \(y = \tan x\), \(y = \cot x\) là hàm số tuần hoàn với chu kỳ \(T = \pi \). Lời giải Hàm số \(y = \tan x\), \(y = \cot x\) là hàm số tuần hoàn với chu kỳ \(T = \pi \). Hàm số \(y = \cos x\) là hàm số tuần hoàn với chu kỳ \(T = 2\pi \). Đáp án B Câu 6: Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \cos 2x + \cos x.\) Khi đó \(M + m\) bằng bao nhiêu?
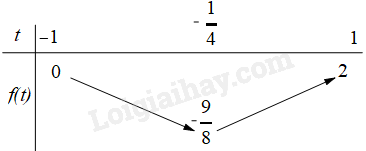
Phương pháp B1: Sử dụng công thức \(\cos 2x = 2{\cos ^2}x - 1\). B2: Đưa hàm số về dạng \(y = 2{\cos ^2}x + \cos x - 1\) sau đó đặt ẩn phụ và khảo sát hàm số. Lời giải TXĐ : \(D = \mathbb{R}\). Ta có: \(y = \cos 2x + \cos x = 2{\cos ^2} + \cos x - 1\). Đặt : \(t = \cos x\), \(t \in \left[ { - 1;1} \right]\). Xét\(f\left( t \right) = 2{t^2} + t - 1\). Đồ thị của hàm số \(f\) là parabol có đỉnh \(I\left( { - \frac{1}{4}; - \frac{9}{8}} \right)\). BBT:
Dựa vào BBT ta có : \(M = \mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = 2\), \(m = \mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = - \frac{9}{8}\). Vậy \(M + m = \frac{7}{8}\). Đáp án A Câu 7: Nghiệm của phương trình \(\cos \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) là:
Phương pháp - Trường hợp \(\left| m \right| > 1\) phương trình vô nghiệm. - Trường hợp \(\left| m \right| \le 1\), khi đó: Tồn tại duy nhất một số thực \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\cos \alpha = m\). Ta có : \(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.,\left( {k \in \mathbb{Z}} \right)\). Lời giải Phương trình \(\cos \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2} \Leftrightarrow \cos \left( {x + \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right) \Rightarrow \left[ \begin{array}{l}x = k2\pi \\x = - \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\). Đáp án D Câu 8: Số nghiệm của phương trình \(\cos x = \frac{1}{2}\) thuộc đoạn \(\left[ { - 2\pi ;2\pi } \right]\) là:
Phương pháp Áp dụng các công thức giải phương trình lượng giác cơ bản rồi kết hợp điều kiện đã cho để chọn nghiệm thỏa mãn. Lời giải Ta có: \(\cos x = \frac{1}{2}\)\( \Leftrightarrow \)\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = - \frac{\pi }{3} + k2\pi \end{array} \right.\), \(k \in \mathbb{Z}\). Xét \(x = \frac{\pi }{3} + k2\pi \), do \(x \in \left[ { - 2\pi ;2\pi } \right]\) và \(k \in \mathbb{Z}\) nên \( - 2\pi \le \frac{\pi }{3} + k2\pi \le 2\pi \)\( \Rightarrow k = - 1\); \(k = 0\). Xét \(x = - \frac{\pi }{3} + k2\pi \), do \(x \in \left[ { - 2\pi ;2\pi } \right]\) và \(k \in \mathbb{Z}\) nên \( - 2\pi \le - \frac{\pi }{3} + k2\pi \le 2\pi \)\( \Rightarrow k = 1\); \(k = 0\). Vậy phương trình có \(4\) nghiệm trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\). Đáp án A Câu 9: Cho dãy số có các số hạng đầu là:\(5;10;15;20;25;...\) Số hạng tổng quát của dãy số này là:
Phương pháp Tìm tính chất chung của các số trong dãy số rồi dự đoán công thức tổng quát. Lời giải Ta có: \(5 = 5.1\) \(10 = 5.2\) \(15 = 5.3\) \(20 = 5.4\) \(25 = 5.5\) Suy ra số hạng tổng quát \({u_n} = 5n\). Đáp án B Câu 10: Cho dãy số \(SC\), biết \(AD\). Ba số hạng đầu tiên của dãy số là:
Phương pháp Thay lần lượt \(n = 1,2,3\) vào công thức \({u_n}\). Lời giải Ta có: \({u_1} = \frac{1}{{{2^1} - 1}} = 1;{u_2} = \frac{2}{{{2^2} - 1}} = \frac{2}{3};{u_3} = \frac{3}{{{2^3} - 1}} = \frac{3}{7}\). Đáp án D Câu 11: Trong các dãy số sau, dãy số nào là một cấp số cộng?
Phương pháp Để chứng minh dãy số \(\left( {{u_n}} \right)\) là một cấp số cộng, ta xét \(A = {u_{n + 1}} - {u_n}\) \( \bullet \) Nếu \(A\) là hằng số thì \(\left( {{u_n}} \right)\) là một cấp số cộng với công sai \(d = A\). \( \bullet \) Nếu \(A\) phụ thuộc vào \(n\) thì \(\left( {{u_n}} \right)\) không là cấp số cộng. Lời giải Ta thấy dãy số: \(1; - 3; - 7; - 11; - 15\) là một cấp số cộng có số hạng đầu là 1 và công sai bằng \( - 4.\) Đáp án C Câu 12: Xác định số hàng đầu \({u_1}\) và công sai \(d\) của cấp số cộng \(\left( {{u_n}} \right)\) có \({u_9} = 5{u_2}\) và \({u_{13}} = 2{u_6} + 5\).
Phương pháp Dựa vào giả thuyết, ta lập một hệ phương trình chứa công sai d và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được d và \({u_1}\). Lời giải Ta có: \({u_n} = {u_1} + \left( {n - 1} \right)d\). Theo đầu bài ta có hpt: \(\left\{ \begin{array}{l}{u_1} + 8d = 5\left( {{u_1} + d} \right)\\{u_1} + 12d = 2\left( {{u_1} + 5d} \right) + 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4{u_1} - 3d = 0\\{u_1} - 2d = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 3\\d = 4\end{array} \right.\). Đáp án A Câu 13: Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa \(\left\{ \begin{array}{l}{u_2} - {u_3} + {u_5} = 10\\{u_4} + {u_6} = 26\end{array} \right.\). Tính \(S = {u_1} + {u_4} + {u_7} + ... + {u_{2011}}\)
Phương pháp Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai \(d\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\) hoặc \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d\) . Lời giải Ta có: \(\left\{ \begin{array}{l}{u_2} - {u_3} + {u_5} = 10\\{u_4} + {u_6} = 26\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} + d - {u_1} - 2d + {u_1} + 4d = 10\\{u_1} + 3d + {u_1} + 5d = 26\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} + 3d = 10\\2{u_1} + 8d = 26\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 1\\d = 3\end{array} \right.\). Ta có: \({u_1}\), \({u_4}\), \({u_7}\), \({u_{10}}\), …,\({u_{2011}}\) là cấp số cộng có \(\left\{ \begin{array}{l}{u_1} = 1\\d = 9\\n = 671\end{array} \right.\) Do đó: \(S = \frac{{671}}{2}\left( {2.1 + 670.9} \right) = 2023736\). Đáp án A Câu 14: Dãy số nào sau đây không phải là cấp số nhân?
Phương pháp Chứng minh \(\forall n \ge 1,{u_{n + 1}} = {u_n}.q\) trong đó \(q\) là một số không đổi. Nếu \({u_n} \ne 0\) với mọi \(n \in {\mathbb{N}^*}\) thì ta lập tỉ số \(T = \frac{{{u_{n + 1}}}}{{{u_n}}}\). \( * \) T là hằng số thì \(({u_n})\) là cấp số nhân có công bội \(q = T\). \( * \) T phụ thuộc vào n thì \(({u_n})\) không là cấp số nhân. Lời giải Dãy \(1\,;\,2\,;\,4\,;\,8\,;\,16\) là cấp số nhân với công bội \(q = 2\). Dãy \(1\,;\, - 1\,;\,1\,;\, - 1\,;\,1\) là cấp số nhân với công bội \(q = - 1\). Dãy \(1\,;\, - 2\,;\,4\,;\, - 8\,;\,16\) là cấp số nhân với công bội \(q = - 2\). Dãy \(1\,;\, - 3\,;\,9\,;\, - 27\,;\,54\) không phải là cấp số nhân vì \( - 3 = 1.( - 3)\,;\,( - 27).( - 3) = 81 \ne 54\). Đáp án A Câu 15: Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \(\left\{ \begin{array}{l}{u_4} - {u_2} = 54\\{u_5} - {u_3} = 108\end{array} \right.\). Tìm số hạng đầu \({u_1}\) và công bội \(q\) của cấp số nhân trên.
Phương pháp Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được q và \({u_1}\). Lời giải Ta có : \(\left\{ \begin{array}{l}{u_4} - {u_2} = 54\\{u_5} - {u_3} = 108\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^3} - {u_1}q = 54\\{u_1}{q^4} - {u_1}{q^2} = 108\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1}q\left( {{q^2} - 1} \right) = 54\\{u_1}{q^2}\left( {{q^2} - 1} \right) = 108\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 9\\q = 2\end{array} \right.\). Vậy \({u_1} = 9\); \(q = 2\). Đáp án A Câu 16: Giá trị của tổng \(4 + 44 + 444 + ... + 44...4\) bằng:
Phương pháp Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}},q \ne 1\). Lời giải Đặt \(S = 4 + 44 + 444 + ... + 44...4\). Ta có:\(\frac{9}{4}S = 9 + 99 + 999 + ... + 99...9\)\( = \left( {10 - 1} \right) + \left( {{{10}^2} - 1} \right) + \left( {{{10}^3} - 1} \right) + ...\left( {{{10}^{2018}} - 1} \right)\) Suy ra: \(\frac{9}{4}S = \)\(\left( {10 + {{10}^2} + {{10}^3} + ... + {{10}^{2018}}} \right) - 2018\). Đặt \(A = 10 + {10^2} + {10^3} + ... + {10^{2018}}\). Ta có: \(A = 10 + {10^2} + {10^3} + ... + {10^{2018}}\) là tổng \(2018\) số hạng của một cấp số nhân có số hạng đầu \({u_1} = 10\), công bội \(q = 10\) nên ta có \(A = {u_1}\frac{{1 - {q^{2018}}}}{{1 - q}}\)\( = 10\frac{{1 - {{10}^{2018}}}}{{ - 9}}\)\( = \frac{{{{10}^{2019}} - 10}}{9}\). Do đó \(\frac{9}{4}S = \frac{{{{10}^{2019}} - 10}}{9} - 2018\)\( \Leftrightarrow S = \frac{4}{9}\left( {\frac{{{{10}^{2019}} - 10}}{9} - 2018} \right)\). Đáp án B Câu 17: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm \([20;40)\) là:
Phương pháp Đọc bảng số liệu. Lời giải Giá trị đại diện của nhóm \([20;40)\) là: \(\frac{{20 + 40}}{2} = 30\). Đáp án C Câu 18: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
Phương pháp Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\). \(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\) trong đó, \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1, \ldots ,k\) ) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\). Lời giải Số trung bình của mẫu số liệu xấp xỉ bằng: \(\left( {6.2 + 8.7 + 10.7 + 12.3 + 14.1} \right):20 = 9,4\) Đáp án B Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
Phương pháp Để tính tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó, \({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\) trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). Lời giải Tứ phân vị thứ nhất của dãy số liệu là \(\frac{1}{2}\left( {{x_4} + {x_5}} \right)\) thuộc nhóm \(\left[ {7;9} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu là \({Q_1} = 7 + \frac{{\frac{{20}}{4} - 2}}{7}\left( {9 - 7} \right) = 7,86\). Đáp án B Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
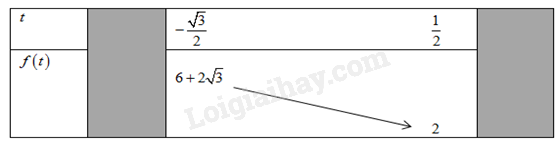
Phương pháp Trung vị là giá trị ở giữa của mẫu số liệu. Lời giải Gọi \({x_1};{x_2};{x_3}; \ldots ;{x_{20}}\) lần lượt là thời gian chạy của các vận động viên theo thứ tự từ nhỏ đến lớn. Do \({x_1},{x_2} \in \left[ {5;7} \right);{x_3}, \ldots ,{x_9} \in \left[ {7;9} \right);{x_{10}}, \ldots ,{x_{16}} \in \left[ {9;11} \right);{x_{17}}, \ldots ,{x_{19}} \in \left[ {11;13} \right)\); \({x_{20}} \in \left[ {13;15} \right)\). Trung vị của mẫu số liệu là \({x_{10}}, \ldots ,{x_{16}}\) thuộc nhóm \(\left[ {9;11} \right)\). Đáp án B Phần tự luận. Bài 1. ( 1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = 4{\cos ^2}x - 4\cos x + 3\) với \(x \in \left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\). Phương pháp B1: Đặt ẩn phụ và tìm điều kiện của ẩn B2: Lập bảng biến thiên, khảo sát hàm số rồi kết luận Lời giải Đặt \(t = \cos x\). Với \(\frac{\pi }{3} \le x \le \frac{{5\pi }}{6}\) ta có \(\frac{{ - \sqrt 3 }}{2} \le t \le \frac{1}{2}\) . Khi đó ta có \(y = f\left( t \right) = 4{t^2} - 4t + 3\) , \(\frac{{ - \sqrt 3 }}{2} \le t \le \frac{1}{2}\). Ta có bảng biến thiên:
Từ bảng biến thiên ta có: Giá trị lớn nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\) là \(6 + 2\sqrt 3 \). Giá trị nhỏ nhất của hàm số đã cho trên \(\left[ {\frac{\pi }{3};\,\frac{{5\pi }}{6}} \right]\) là \(2\). Bài 2. (1.5 điểm) a) Giải phương trình \(\sin \left( {\frac{x}{2} - \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{4}\) b) Tìm nghiệm thuộc khoảng \(\left( { - \frac{\pi }{4};2\pi } \right)\) của phương trình \(\sin \left( {\frac{\pi }{6} + 2x} \right) = - 1\). c) Giải phương trình sau: \(\cos \,x + \cos \,2x + \cos \,3x = 0\). Phương pháp a) - Trường hợp \(\left| m \right| > 1\), phương trình vô nghiệm. - Trường hợp \(\left| m \right| \le 1\), tồn tại duy nhất một số \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thỏa mãn \(\sin \alpha = m\). Ta có \(\sin x = \sin \alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.,\left( {k \in \mathbb{Z}} \right)\). b) Áp dụng các công thức giải phương trình lượng giác cơ bản rồi kết hợp điều kiện đã cho để chọn nghiệm thỏa mãn. c) Sử dụng công thức biến tổng thành tính để làm xuất hiện nhân tử chung: \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\). Lời giải a) Ta có: \(\sin \left( {\frac{x}{2} - \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{4}\) đặt \(\sin t = - \frac{{\sqrt 3 }}{4}\)\( \Rightarrow \sin \left( {\frac{x}{2} - \frac{\pi }{3}} \right) = \sin t \Rightarrow \left[ {\begin{array}{*{20}{c}}{\frac{x}{2} - \frac{\pi }{3} = t + k2\pi }\\{\frac{x}{2} - \frac{\pi }{3} = \pi - t + k2\pi }\end{array} \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{x = \frac{{2\pi }}{3} + 2t + k4\pi }\\{x = \frac{{8\pi }}{3} - 2t + k4\pi }\end{array}} \right.\). b) Ta có: \(\sin \left( {\frac{\pi }{6} + 2x} \right) = - 1 \Leftrightarrow \frac{\pi }{6} + 2x = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = - \frac{\pi }{3} + k\pi \). Theo để bài, ta có: \( - \frac{\pi }{4} < - \frac{\pi }{3} + k\pi < 2\pi \Rightarrow k = 1;2 \Rightarrow x = \frac{{2\pi }}{3};\frac{{5\pi }}{3}.\) c) Ta có: \(\cos \,x + \cos \,2x + \cos \,3x = 0\) \( \Leftrightarrow 2\cos \,\left( {\frac{{x + 3x}}{2}} \right).\cos \,\left( {\frac{{x - 3x}}{2}} \right) + \cos \,2x = 0\) \( \Leftrightarrow 2\cos \,2x.\cos \,x + \cos \,2x = 0\) \( \Leftrightarrow \cos \,2x\left( {2\cos \,x + 1} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}\cos \,2x = 0\\\cos \,x = \frac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k\frac{\pi }{2}\\x = \frac{{2\pi }}{3} + k2\pi \\x = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\). Bài 3. (2 điểm) a) Cho cấp số cộng \(\left( {{u_n}} \right)\)có \({u_1} = - 2\) và \(d = 3\). Biết \({S_n} = 6095374\), tìm \(n\). b) Tìm số hạng đầu tiên và công bội của cấp số nhân sau, biết rằng: \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\). Phương pháp a) Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai \(d\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\) hoặc \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d\) . b) Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được q và \({u_1}\). Lời giải a) Ta có : \({S_n} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d = - 2n + \frac{{3\left( {{n^2} - n} \right)}}{2} = \frac{{n\left( {3n - 7} \right)}}{2}\) Vì \({S_n} = 6095374\) nên \(\frac{{n\left( {3n - 7} \right)}}{2} = 6095374 \Leftrightarrow 3{n^2} - 7n - 12190748 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 2017\\n = - \frac{{6044}}{3}\end{array} \right.\). Vậy \(n = 2017\). b) Ta có : \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + {u_1}{q^4} = 51\\{u_1}q + {u_1}{q^5} = 102\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}\left( {1 + {q^4}} \right) = 51{\rm{ }}\left( * \right)\\{u_1}q\left( {1 + {q^4}} \right) = 102{\rm{ }}\left( {**} \right)\end{array} \right.\). Lấy\(\frac{{\left( {**} \right)}}{{\left( * \right)}} \Leftrightarrow \frac{{{u_1}q\left( {1 + {q^4}} \right)}}{{{u_1}\left( {1 + {q^4}} \right)}} = \frac{{102}}{{51}}\) \( \Leftrightarrow q = 2 \Rightarrow {u_1} = \frac{{51}}{{1 + {q^4}}} = \frac{{51}}{{17}} = 3.\) Kết luận có công bội \(q = 2\)và số hạng đầu tiên \({u_1} = 3\). Bài 4. ( 1.5 điểm) Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên.
a) Tính trung vị của mẫu số liệu ghép nhóm này.
b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này. Phương pháp a) Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau: Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Bước 2. Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right)\), trong đó \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\). Với \(p = 1\), ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). b) Để tính tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó, \({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\) trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). Để tính tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\). Giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó, \({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\) trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). Tứ phân vị thứ hai \({Q_2}\) chính là trung vị \({M_e}\). Nhận xét. Ta cũng có thể xác định nhóm chứa tứ phân vi thứ \(r\) nhờ tính chất: có khoảng \(\left( {\frac{{r \cdot n}}{4}} \right)\) giá trị nhỏ hơn tứ phân vị này. Lời giải a) Cỡ mẫu là: \(n = 18 + 28 + 35 + 43 + 43 + 41 + 35 = 200\). Gọi \({x_1},{x_2} \ldots {x_{200}}\) là tốc độ giao bóng của 200 lần và giả sử dãy này được sắp xếp theo thứ tự tăng dần. Khi đó trung vị là \(\frac{{{x_{100}} + {x_{101}}}}{2}\). Do hai giá trị \({x_{100}},{x_{101}}\) thuộc nhóm [165;170) nên nhóm này chứa trung vị. Suy ra, \(p = 4;{a_4} = 165;{m_4} = 43;{m_1} + {m_2} + {m_3} = 18 + 28 + 35 = 81;{a_5} - {a_4} = 5\) và ta có: \({M_e} = 165 + \frac{{\frac{{200}}{2} - 81}}{{43}} \times 5 = 167,21\). b) Cỡ mẫu: \(n = 200\). Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{50}} + {x_{51}}}}{2}\). Do \({x_{50}};{x_{51}}\) đều thuộc nhóm [160;165) nên tứ phân vị thứ nhất thuộc nhóm [160;165). Do đó, \(p = 3;{a_3} = 160;{m_3} = 35;{m_1} + {m_2} = 18 + 28 = 46;{a_4} - {a_3} = 5\) và ta có: \({Q_1} = 160 + \frac{{\frac{{200}}{4} - 46}}{{35}} \times 5 = 160,57\). Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{150}} + {x_{151}}}}{2}\). Do \({x_{150}},{x_{151}}\) đều thuộc nhóm [170;175) nên tứ phân vị thứ ba thuộc nhóm [170;175). Do đó,\(p = 5;{a_5} = 170;{m_5} = 41;{m_1} + {m_2} + {m_3} + {m_4} = 18 + 28 + 35 + 43 = 124;{a_6} - {a_5} = 5\) và ta có: \({Q_3} = 170 + \frac{{\frac{{600}}{4} - 124}}{{41}} \times 5 = 173,17\).
|



























Danh sách bình luận