Đề thi học kì 2 Toán 11 - Đề số 7Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.Đề bài
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Tìm tập xác định \(D\) của hàm số \(y = \ln \left( { - {x^2} - 3x + 4} \right)\)
Câu 2 :
Cho hai đường thẳng phân biệt \(a;{\mkern 1mu} {\mkern 1mu} b\) và mặt phẳng \(\left( P \right)\), trong đó \(a \bot \left( P \right)\). Mệnh đề nào sau đây là sai?
Câu 3 :
Nghiệm của phương trình \({3^{x - 2}} = 9\) là
Câu 4 :
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {{x^2} - 3x} \right)\left[ {{{\log }_2}\left( {x + 25} \right) - 6} \right] < 0\)?
Câu 5 :
Cho bất phương trình \({\left( {\frac{2}{3}} \right)^{{x^2} - x + 1}} > {\left( {\frac{2}{3}} \right)^{2x - 1}}\) có tập nghiệm \(S = \left( {a;b} \right)\). Giá trị của \(b - a\) bằng
Câu 6 :
Năm 2024 , một hãng xe ô tô niêm yết giá bán loại xe \(X\) là 900.000 .000 đồng và dự định trong 10 năm tiếp theo, mỗi năm giảm \(2\% \) giá bán so với giá bán năm trước. Theo dự định đó, năm 2029 hãng xe ô tô niêm yết giá bán loại xe \(X\) là bao nhiêu (kết quả làm tròn đến hàng nghìn)?
Câu 7 :
Đạo hàm của hàm số \(y = 4\sqrt x {\rm{ \;}} - \frac{5}{x}\) bằng biểu thức nào dưới đây?
Câu 8 :
Một hộp có 30 tấm thẻ được đánh số từ 1 đến 30. Lấy ngẫu nhiên một tấm thẻ từ hộp. Xét các biến cố sau: \(P\) : "Số ghi trên thẻ được lấy là số chia hết cho 2". \(Q\) : "Số ghi trên thẻ được lấy là số chia hết cho 4". Khi đó biến cố \(P \cap Q\) là
Câu 9 :
Cho \(A,{\mkern 1mu} {\mkern 1mu} B\) là hai biến cố độc lập cùng liên quan đến phép thử \(T\), xác suất xảy ra biến cố \(A\) là \(\frac{1}{2}\), xác suất xảy ra biến cố \(B\) là \(\frac{1}{4}\). Xác suất để xảy ra biến cố \(A\) và \(B\) là:
Câu 10 :
Cho hình chóp đều S.ABCD có cạnh đáy bằng \(a\). Biết khoảng cách giữa hai đường thẳng AC và SD bằng \(\frac{{a\sqrt {30} }}{{10}}\). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
Câu 11 :
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\), tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD theo \(a\)
Câu 12 :
Một vật rơi tự do theo phương trình \(s = \frac{1}{2}g{t^2}{\mkern 1mu} {\mkern 1mu} \left( m \right)\), với \(g = {\rm{\;}}9,8{\mkern 1mu} {\mkern 1mu} \left( {m/{s^2}} \right)\). Vận tốc tức thời tại thời điểm \(t = 5{\mkern 1mu} {\mkern 1mu} \left( s \right)\) là:
Câu 13 :
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} + 2x - \frac{3}{2}\). Tìm tập nghiệm \(S\) của bất phương trình \(f'\left( x \right) = 0\)
Câu 14 :
Đạo hàm của hàm số \(f(x) = \sqrt {{x^2} - 5x} \) bằng
Câu 15 :
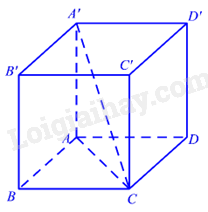
Cho hình hộp chữ nhật ABCD.A'B'C'D' có \(AB = BC = a,{\mkern 1mu} AA' = \sqrt 6 a\) (tham khảo hình dưới). Góc giữa đường thẳng A'C và mặt phẳng \(\left( {ABCD} \right)\) bằng:
Câu 16 :
Cho \({\rm{A}}\) và \({\rm{B}}\) là 2 biến cố độc lập với nhau, \({\rm{P}}\left( {\rm{A}} \right) = 0,4;{\rm{P}}\left( {\rm{B}} \right) = 0,3\). Khi đó \({\rm{P}}\left( {{\rm{A}} \cdot {\rm{B}}} \right)\) bằng
Câu 17 :
Một cầu thủ sút bóng vào cầu môn. Xác suất sút thành công của cầu thủ đó là \(\frac{3}{7}\). Xác suất để trong 2 lần sút, cầu thủ sút thành công ít nhất 1 lần là:
Câu 18 :
Cho chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = {\rm{ \;}} - {t^3} + 6{t^2} + t{\mkern 1mu} \left( m \right)\). Vận tốc lớn nhất của chuyển động trên là:
Câu 19 :
Tính đạo hàm của hàm số \(f\left( x \right) = {\sin ^2}2x - c{\rm{os3x}}\)
Câu 20 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng \(SA = SC,SB = SD.\) Khẳng định nào sau đây đúng?
Câu 21 :
Cho \(f(x) = 3{x^2}\); \(g(x) = 5(3x - {x^2})\). Bất phương trình \(f'\left( x \right) > g'\left( x \right)\) có tập nghiệm là
Câu 22 :
Ba người cùng bắn vào một bia một cách độc lập. Xác suất để người thứ nhất, thứ hai, thứ ba bắn trúng đích lần lượt là 0,5;0,6; và 0,8 . Xác suất để có đúng 2 người bắn trúng đích là
Câu 23 :
Cho A,B là hai biến cố. Biết \({\rm{P}} = \frac{1}{2},{\rm{P}}\left( B \right) = \frac{3}{4};{\rm{P}}\left( {A \cap B} \right) = \frac{1}{4}\). Biến cố \(A \cup B\) là biến cố
Câu 24 :
Cho khối chóp S.ABC có đáy là tam giác đều cạnh \(a\) và thể tích khối chóp \(\frac{{{a^3}}}{4}\). Tính khoảng cách từ \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
Câu 25 :
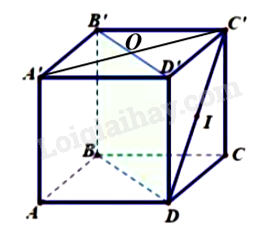
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) cạnh \(a\). I là trung điểm CD'. Khoảng cách từ \(I\) dến mặt phằng \(\left( {BDD'B'} \right)\) bằng
Câu 26 :
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} + x\), biết tiếp tuyến đó vuông góc với đường thẳng \(y = {\rm{ \;}} - \frac{1}{5}x + 2\).
Câu 27 :
Cho khối hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có đáy là hình vuông, \(BD = 2a\), góc phẳng nhị diện \(\left[ {A',BD,A} \right]\) bằng \(30^\circ \). Tính độ dài cạnh AA'
Câu 28 :
Kim tự tháp Kê - ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao là 147m, cạnh đáy là 230m. Thể tích của nó là
Câu 29 :
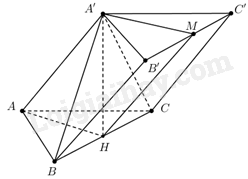
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại \(A\), góc giữa A'C với mặt đáy \(\left( {ABC} \right)\) bằng \(45^\circ \) và \(AA' = 4\). Gọi \(M\) là trung điểm của CC'. Khoảng cách từ \(M\) đến mặt phẳng \(\left( {A'BC} \right)\) bằng
Câu 30 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với mặt đáy và \(SA = \frac{{a\sqrt 6 }}{6}\). Khi đó số đo của góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là
Câu 31 :
Tổng tất cả các nghiệm của phương trình \({9^x} - {4.3^x} + 3 = 0\) bằng
Câu 32 :
Trong một lớp 10 có 50 học sinh. Khi đăng ký cho học phụ đạo thì có 38 học sinh đăng ký học Toán, 30 học sinh đăng ký học Lý, 25 học sinh đăng ký học cả Toán và Lý. Nếu chọ ngẫu nhiên 1 học sinh của lớp đó thì xác suất để em này không đăng ký học phụ đạo môn nào cả là bao nhiêu
Câu 33 :
Cho khối lăng trụ \(ABC \cdot A'B'C'\) có đáy ABC là tam giác vuông cân tại \(A\), \(A'A = A'B = A'C = a\). Biết góc giữa hai mặt phẳng \(\left( {BCC'B'} \right)\) và \(\left( {ABC} \right)\) bằng \(30^\circ \), thể tích của khối lăng trụ đã cho bằng
Câu 34 :
Tìm số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{3}}}\left( {4x - 9} \right) > {\log _{\frac{1}{3}}}\left( {x + 10} \right)\)
Câu 35 :
Tìm \(m\) để hàm số \(y = \frac{{m{x^3}}}{3} - m{x^2} + \left( {3m - 1} \right)x + 1\) có \(y' \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R\)
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Tìm tập xác định \(D\) của hàm số \(y = \ln \left( { - {x^2} - 3x + 4} \right)\)
Đáp án : B Phương pháp giải :
Hàm số \(y = \ln \left( {f\left( x \right)} \right)\) xác định khi \(f\left( x \right) > 0\) Lời giải chi tiết :
Hàm số đã cho xác định khi \( - {x^2} - 3x + 4 > 0 \Leftrightarrow {x^2} + 3x - 4 < 0 \Leftrightarrow {\rm{ \;}} - 4 < x < 1\) Đáp án B.
Câu 2 :
Cho hai đường thẳng phân biệt \(a;{\mkern 1mu} {\mkern 1mu} b\) và mặt phẳng \(\left( P \right)\), trong đó \(a \bot \left( P \right)\). Mệnh đề nào sau đây là sai?
Đáp án : D Phương pháp giải :
Dùng tính chất, quan hệ giữa vuông góc và song song: Cho hai đường thẳng phân biệt \(a;{\mkern 1mu} {\mkern 1mu} b\) và mặt phẳng \(\left( P \right)\), trong đó \(a \bot \left( P \right)\). Khi đó: Nếu \(b//{\mkern 1mu} {\mkern 1mu} \left( P \right){\mkern 1mu} \) thì \(b \bot a\) Nếu \(b//a\) thì \(b \bot \left( P \right)\). Nếu \(b \bot \left( P \right)\) thì \(b//a\). Lời giải chi tiết :
Cho hai đường thẳng phân biệt \(a;{\mkern 1mu} {\mkern 1mu} b\) và mặt phẳng \(\left( P \right)\), trong đó \(a \bot \left( P \right)\). Mệnh đề: nếu \(b \bot a\) thì \(b//{\mkern 1mu} \left( P \right)\) là sai vì có thể \(b\) nằm trong \(\left( P \right)\). Đáp án D.
Câu 3 :
Nghiệm của phương trình \({3^{x - 2}} = 9\) là
Đáp án : C Phương pháp giải :
Giải phương trình Lời giải chi tiết :
Ta có: \({3^{x - 2}} = 9 \Leftrightarrow x - 2 = 2 \Leftrightarrow x = 4\) Đáp án C.
Câu 4 :
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {{x^2} - 3x} \right)\left[ {{{\log }_2}\left( {x + 25} \right) - 6} \right] < 0\)?
Đáp án : D Phương pháp giải :
Chia trường hợp giải bất phương trình Lời giải chi tiết :
\(({x^2} - 3x)\)\(\left[ {{{\log }_2}(x + 25) - 6} \right] < 0\) TH1: \(\left\{ {\begin{array}{*{20}{l}}{x > {\rm{ \;}} - 25}\\{{x^2} - 3x > 0}\\{{{\log }_2}(x + 25) - 6 < 0}\end{array}} \right. \Leftrightarrow x \in ( - 25;0) \cup (3;39)\) có 59 giá trị x nguyên. TH2:\(\left\{ {\begin{array}{*{20}{l}}{x > {\rm{ \;}} - 25}\\{{x^2} - 3x < 0}\\{{{\log }_2}(x + 25) - 6 > 0}\end{array}} \right. \Leftrightarrow VN\) Vậy có 59 giá trị x nguyên thỏa mãn yêu cầu đề bài. Đáp án D.
Câu 5 :
Cho bất phương trình \({\left( {\frac{2}{3}} \right)^{{x^2} - x + 1}} > {\left( {\frac{2}{3}} \right)^{2x - 1}}\) có tập nghiệm \(S = \left( {a;b} \right)\). Giá trị của \(b - a\) bằng
Đáp án : C Phương pháp giải :
\({a^x} > {a^y} \Leftrightarrow x > y\) nếu \(a > 1\) \({a^x} > {a^y} \Leftrightarrow x < y\) nếu \(0 < a < 1\) Lời giải chi tiết :
\({\left( {\frac{2}{3}} \right)^{{x^2} - x + 1}} > {\left( {\frac{2}{3}} \right)^{2x - 1}} \Leftrightarrow {x^2} - x + 1 < 2x - 1 \Leftrightarrow {x^2} - 3x + 2 < 0 \Leftrightarrow 1 < x < 2\) \( \Rightarrow a = 1;b = 2 \Rightarrow b - a = 1\) Đáp án C.
Câu 6 :
Năm 2024 , một hãng xe ô tô niêm yết giá bán loại xe \(X\) là 900.000 .000 đồng và dự định trong 10 năm tiếp theo, mỗi năm giảm \(2\% \) giá bán so với giá bán năm trước. Theo dự định đó, năm 2029 hãng xe ô tô niêm yết giá bán loại xe \(X\) là bao nhiêu (kết quả làm tròn đến hàng nghìn)?
Đáp án : B Phương pháp giải :
Áp dụng công thức \({T_1} = A - Ar\) Lời giải chi tiết :
Ta có: \(A = 900.000.000,r = \frac{2}{{100}}\) Năm 2025 giá xe niêm yết là: \({T_1} = A - Ar\) Năm 2026 giá xe niêm yết là \({T_2} = A - Ar - (A - Ar)r = A{(1 - r)^2}\) Năm 2029 giá xe niêm yết là: \({T_5} = {T_4} - {T_4}r = A{(1 - r)^3}\) \({T_5} = 900.000.000{\left( {1 - \frac{2}{{100}}} \right)^5} \approx 813.529.000\) Đáp án B.
Câu 7 :
Đạo hàm của hàm số \(y = 4\sqrt x {\rm{ \;}} - \frac{5}{x}\) bằng biểu thức nào dưới đây?
Đáp án : D Phương pháp giải :
Sử dụng bảng đạo hàm cơ bản. Lời giải chi tiết :
\(y = 4\sqrt x {\rm{ \;}} - \frac{5}{x} \Rightarrow y' = 4.\frac{1}{{2\sqrt x }} + \frac{5}{{{x^2}}} = \frac{2}{{\sqrt x }} + \frac{5}{{{x^2}}}\). Đáp án D.
Câu 8 :
Một hộp có 30 tấm thẻ được đánh số từ 1 đến 30. Lấy ngẫu nhiên một tấm thẻ từ hộp. Xét các biến cố sau: \(P\) : "Số ghi trên thẻ được lấy là số chia hết cho 2". \(Q\) : "Số ghi trên thẻ được lấy là số chia hết cho 4". Khi đó biến cố \(P \cap Q\) là
Đáp án : D Phương pháp giải :
Theo định nghĩa, biến cố "Cả \(A\) và \(B\) đều xảy ra" được gọi là biến cố giao của \(A\) và \(B\). Lời giải chi tiết :
Biến cố \(P \cap Q\) : "Số ghi trên thẻ được lấy là số chia hết cho cả 2 và 4", tức là chia hết cho 4. Đáp án D.
Câu 9 :
Cho \(A,{\mkern 1mu} {\mkern 1mu} B\) là hai biến cố độc lập cùng liên quan đến phép thử \(T\), xác suất xảy ra biến cố \(A\) là \(\frac{1}{2}\), xác suất xảy ra biến cố \(B\) là \(\frac{1}{4}\). Xác suất để xảy ra biến cố \(A\) và \(B\) là:
Đáp án : A Phương pháp giải :
\(A,{\mkern 1mu} {\mkern 1mu} B\) là hai biến cố độc lập thì \(P\left( {A.B} \right) = P\left( A \right).P\left( B \right)\). Lời giải chi tiết :
Vì \(A,{\mkern 1mu} {\mkern 1mu} B\) là hai biến cố độc lập thì \(P\left( {A.B} \right) = P\left( A \right).P\left( B \right) = \frac{1}{2}.\frac{1}{4} = \frac{1}{8}\). Đáp án A.
Câu 10 :
Cho hình chóp đều S.ABCD có cạnh đáy bằng \(a\). Biết khoảng cách giữa hai đường thẳng AC và SD bằng \(\frac{{a\sqrt {30} }}{{10}}\). Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
Đáp án : D Phương pháp giải :
Đưa về khoảng cách từ O đến (CSD) Lời giải chi tiết :
Kẻ \(OH \bot SD\) Ta có \(AC \bot BD\) (tính chất hình vuông) và \(AC \bot SO \Rightarrow AC \bot \left( {SBD} \right) \Rightarrow AC \bot OH\) \( \Rightarrow OH\) là đường vuông góc chung của AC và SD \( \Rightarrow OH = \frac{{a\sqrt {30} }}{{10}} \Rightarrow \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{D^2}}} = \frac{4}{3} \Rightarrow SO = \frac{{\sqrt 3 }}{2}a\) Gọi M là trung điểm của CD, kẻ \(ON \bot SM\) \( \Rightarrow d\left( {O,CSD} \right) = ON\) \( \Rightarrow \frac{1}{{O{N^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} \Rightarrow ON = \frac{{\sqrt 3 }}{4}a\) \( \Rightarrow d\left( {B,CSD} \right) = 2d\left( {O,CSD} \right) = 2.\frac{{\sqrt 3 }}{4}a = \frac{{\sqrt 3 }}{2}a\) Đáp án D.
Câu 11 :
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh \(a\), tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD theo \(a\)
Đáp án : D Phương pháp giải :
- Tính chiều cao của khối chóp - Tính thể tích Lời giải chi tiết :
Gọi \(H\) là trung điểm của AB Vì tam giác SAB đều nên \(SH \bot AB\) và \(SH = \frac{{a\sqrt 3 }}{2}\) Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)\) Thể tích của khối chóp S.ABCD là \(V = \frac{1}{3}.SH.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.{a^2} = \frac{{{a^3}\sqrt 3 }}{6}\) Đáp án D.
Câu 12 :
Một vật rơi tự do theo phương trình \(s = \frac{1}{2}g{t^2}{\mkern 1mu} {\mkern 1mu} \left( m \right)\), với \(g = {\rm{\;}}9,8{\mkern 1mu} {\mkern 1mu} \left( {m/{s^2}} \right)\). Vận tốc tức thời tại thời điểm \(t = 5{\mkern 1mu} {\mkern 1mu} \left( s \right)\) là:
Đáp án : D Phương pháp giải :
Vận tốc tức thời tại thời điểm \(t = {t_0}\) là: \(v\left( {{t_0}} \right) = s'\left( {{t_0}} \right)\). Lời giải chi tiết :
Ta có: \(s' = gt\). Vận tốc tức thời tại thời điểm \(t = 5{\mkern 1mu} \left( s \right)\) là: \(v\left( 5 \right) = s'\left( 5 \right) = 5g = 49{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\). Đáp án D.
Câu 13 :
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} + 2x - \frac{3}{2}\). Tìm tập nghiệm \(S\) của bất phương trình \(f'\left( x \right) = 0\)
Đáp án : C Phương pháp giải :
\(\begin{array}{*{20}{l}}{{{\left( {{x^n}} \right)}^\prime } = n{x^{n - 1}};}\\{{{\left( C \right)}^\prime } = 0}\\{{{\left( {k{x^n}} \right)}^\prime } = k.{\mkern 1mu} {{\left( {{x^n}} \right)}^\prime }}\\{{{\left( {u \pm v} \right)}^\prime } = u' \pm v'}\end{array}\) Lời giải chi tiết :
\(f\left( x \right) = \frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} + 2x - \frac{3}{2}\) Suy ra: \(\begin{array}{*{20}{l}}{f' = {\mkern 1mu} \frac{1}{3}.3{x^2} - \frac{3}{2}.2x + 2 - 0 = {x^2} - 3x + 2}\\{f' = 0 \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 2}\end{array}} \right.}\end{array}\) Vậy \(S = \left\{ {1;{\mkern 1mu} 2} \right\}\). Đáp án C.
Câu 14 :
Đạo hàm của hàm số \(f(x) = \sqrt {{x^2} - 5x} \) bằng
Đáp án : B Phương pháp giải :
Sử dụng công thức tính đạo hàm hàm hợp: \({\left( {\sqrt u } \right)'} = \frac{{u'}}{{2\sqrt u }}\). Lời giải chi tiết :
Ta có: \(\begin{array}{*{20}{l}}{f(x) = \sqrt {{x^2} - 5x} }\\{ \Rightarrow f'\left( x \right) = \frac{{\left( {{x^2} - 5x} \right)'}}{{2\sqrt {{x^2} - 5x} }} = \frac{{2x - 5}}{{2\sqrt {{x^2} - 5x} }}.}\end{array}\) Đáp án B.
Câu 15 :
Cho hình hộp chữ nhật ABCD.A'B'C'D' có \(AB = BC = a,{\mkern 1mu} AA' = \sqrt 6 a\) (tham khảo hình dưới). Góc giữa đường thẳng A'C và mặt phẳng \(\left( {ABCD} \right)\) bằng:
Đáp án : A Phương pháp giải :
\(\left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {A'CA}\) Lời giải chi tiết :
Ta có \(\left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {A'CA}\) Ta có \(AC = \sqrt {A{B^2} + B{C^2}} {\rm{ \;}} = a\sqrt 2 \). Xét tam giác \(\Delta A'CA\) có \(\tan \widehat {A'CA} = \frac{{A'A}}{{AC}} = \frac{{\sqrt 6 a}}{{\sqrt 2 a}} = \sqrt 3 {\rm{ \;}} \Rightarrow \widehat {A'CA} = {60^\circ }\). Vậy góc A'C và mặt phẳng \(\left( {ABCD} \right)\) và bằng \(60^\circ \). Đáp án A.
Câu 16 :
Cho \({\rm{A}}\) và \({\rm{B}}\) là 2 biến cố độc lập với nhau, \({\rm{P}}\left( {\rm{A}} \right) = 0,4;{\rm{P}}\left( {\rm{B}} \right) = 0,3\). Khi đó \({\rm{P}}\left( {{\rm{A}} \cdot {\rm{B}}} \right)\) bằng
Đáp án : D Phương pháp giải :
A,B là hai biến cố độc lập nên: \(P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( B \right)\). Lời giải chi tiết :
Do \(A\) và \(B\) là 2 biến cố độc lập với nhau nên \(P\left( {A \cdot B} \right) = P\left( A \right) \cdot P\left( B \right) = 0,12\) Đáp án D.
Câu 17 :
Một cầu thủ sút bóng vào cầu môn. Xác suất sút thành công của cầu thủ đó là \(\frac{3}{7}\). Xác suất để trong 2 lần sút, cầu thủ sút thành công ít nhất 1 lần là:
Đáp án : A Phương pháp giải :
Sử dụng biến cố đối và phép nhân xác suất. Lời giải chi tiết :
Gọi A là biến cố: “trong 2 lần sút, cầu thủ sút thành công ít nhất 1 lần” \( \Rightarrow \) Biến cố đối \(\bar A\): “trong 2 lần sút, cầu thủ sút không thành công lần nào”, tức là cả hai lần đều sút trượt, khi đó ta có \(P\left( {\bar A} \right) = \frac{4}{7}.\frac{4}{7} = \frac{{16}}{{49}}\). Vậy \(P\left( A \right) = 1 - P\left( {\bar A} \right) = 1 - \frac{{16}}{{49}} = \frac{{33}}{{49}}\). Đáp án A.
Câu 18 :
Cho chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = {\rm{ \;}} - {t^3} + 6{t^2} + t{\mkern 1mu} \left( m \right)\). Vận tốc lớn nhất của chuyển động trên là:
Đáp án : C Phương pháp giải :
Một vật chuyển động có phương trình quãng đường là \(S = S\left( t \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \)thì phương trình vận tốc của chuyển động là \(V\left( t \right) = S'\left( t \right)\). Lời giải chi tiết :
\(s\left( t \right) = {\rm{ \;}} - {t^3} + 6{t^2} + t{\mkern 1mu} \left( m \right)\) Phương trình vận tốc của chuyển động là: \(v\left( t \right) = S'\left( t \right) = {\rm{ \;}} - 3{t^2} + 12t + 1{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\) Ta có \(v\left( t \right) = S'\left( t \right) = {\rm{ \;}} - 3{t^2} + 12t + 1 = {\mkern 1mu} - 3{\left( {t - 2} \right)^2} + 13{\mkern 1mu} {\mkern 1mu} \le 13\). Do đó, vận tốc lớn nhất của chuyển động là \(13{\mkern 1mu} m/s\). Đáp án C.
Câu 19 :
Tính đạo hàm của hàm số \(f\left( x \right) = {\sin ^2}2x - c{\rm{os3x}}\)
Đáp án : A Phương pháp giải :
Áp dụng công thức đạo hàm hàm hợp: \({\left( {{u^n}} \right)'} = n.{u^{n - 1}}.u';{\mkern 1mu} {\mkern 1mu} {\left( {\sin u} \right)'} = u'.c{\rm{osu}};{\mkern 1mu} {\left( {{\rm{cosu}}} \right)'} = {\rm{ \;}} - u'.\sin u\) Công thức nhân đôi \(\sin 2x = 2\sin x.c{\rm{osx}}\). Lời giải chi tiết :
\(\begin{array}{*{20}{l}}{f\left( x \right) = {{\sin }^2}2x - c{\rm{os3x}}}\\{ \Rightarrow f'\left( x \right) = 2\sin 2x.{{\left( {\sin 2x} \right)}'} + \sin 3x.{{\left( {3x} \right)}'} = {\mkern 1mu} {\mkern 1mu} 4\sin 2x.c{\rm{os2x + \;3sin3x = 2sin4x \; + \;3sin3x}}}\end{array}\) Đáp án A.
Câu 20 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng \(SA = SC,SB = SD.\) Khẳng định nào sau đây đúng?
Đáp án : D Phương pháp giải :
Sử dụng tính chất: trong tam giác cân, đường trung tuyến đồng thời là đường cao. Gọi \(O\) là giao điểm hai đường chéo AC và BD. Chỉ ra SO vuông góc với hai đường thẳng cắt nhau của mặt phẳng \(\left( {ABCD} \right)\). Lời giải chi tiết :
Gọi \(O\) là giao điểm hai đường chéo AC và BD. Tam giác SBD cân tại \(S\) có SO là đường trung tuyến \( \Rightarrow SO\) là đường cao \( \Rightarrow SO \bot BD\) Tam giác SAC cân tại \(S\) có SO là đường trung tuyến \( \Rightarrow SO\) là đường cao \( \Rightarrow SO \bot AC\) Suy ra \(SO \bot \left( {ABCD} \right)\) Đáp án D.
Câu 21 :
Cho \(f(x) = 3{x^2}\); \(g(x) = 5(3x - {x^2})\). Bất phương trình \(f'\left( x \right) > g'\left( x \right)\) có tập nghiệm là
Đáp án : D Phương pháp giải :
- Tính đạo hàm của các hàm số, sử dụng công thức \({\left( {{x^n}} \right)'} = n.{x^{n - 1}}\). - Giải bất phương trình bậc nhất một ẩn: \(ax + b > 0 \Leftrightarrow x > {\rm{\;}} - \frac{b}{a}\) \(\left( {a \ne 0} \right)\). Lời giải chi tiết :
Ta có: \(\begin{array}{*{20}{l}}{f'\left( x \right) = 6x}\\{g'\left( x \right) = 5.\left( {3 - 2x} \right) = 15 - 10x}\end{array}\) Khi đó ta có: \(\begin{array}{*{20}{l}}{f'\left( x \right) > g'\left( x \right)}\\{ \Leftrightarrow 6x > 15 - 10x}\\{ \Leftrightarrow 16x > 15}\\{ \Leftrightarrow x > \frac{{15}}{{16}}}\end{array}\) Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{15}}{{16}}; + \infty } \right).\) Đáp án D.
Câu 22 :
Ba người cùng bắn vào một bia một cách độc lập. Xác suất để người thứ nhất, thứ hai, thứ ba bắn trúng đích lần lượt là 0,5;0,6; và 0,8 . Xác suất để có đúng 2 người bắn trúng đích là
Đáp án : B Phương pháp giải :
Chia ra ba trường hợp. Lời giải chi tiết :
Từ giả thiết suy ra xác suất để người thứ nhất, thứ hai, thứ ba bắn không trúng đích lần lượt là 0,5;0,4; và 0,2. Để có đúng 2 người bắn trúng đích thì có các trường hợp sau Trường hợp 1. Người thứ nhất bắn trúng; Người thứ hai bắn trúng; Người thứ ba bắn không trúng. Kết quả: \(0,5 \times 0,6 \times 0,2\). Trường hợp 2. Người thứ nhất bắn trúng; Người thứ hai bắn không trúng; Người thứ ba bắn trúng. Kết quả: \(0,5 \times 0,4 \times 0,8\). Trường hợp 3. Người thứ nhất không bắn trúng; Người thứ hai bắn trúng; Người thứ ba bắn trúng. Kết quả: \(0,5 \times 0,6 \times 0,8\). Vậy xác suất để có đúng 2 người bắn trúng đích là \((0,5 \times 0,6 \times 0,2) + (0,5 \times 0,4 \times 0,8) + (0,5 \times 0,6 \times 0,8) = 0,46.\) Đáp án B.
Câu 23 :
Cho A,B là hai biến cố. Biết \({\rm{P}} = \frac{1}{2},{\rm{P}}\left( B \right) = \frac{3}{4};{\rm{P}}\left( {A \cap B} \right) = \frac{1}{4}\). Biến cố \(A \cup B\) là biến cố
Đáp án : B Phương pháp giải :
A,B là hai biến cố bất kỳ ta luôn có: \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\) Lời giải chi tiết :
A,B là hai biến cố bất kỳ ta luôn có: \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right) = \frac{1}{2} + \frac{3}{4} - \frac{1}{4} = 1\) Vậy \(A \cup B\) là biến cố chắc chắn. Đáp án B.
Câu 24 :
Cho khối chóp S.ABC có đáy là tam giác đều cạnh \(a\) và thể tích khối chóp \(\frac{{{a^3}}}{4}\). Tính khoảng cách từ \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
Đáp án : B Phương pháp giải :
Khoảng cách từ \(S\) đến mặt phẳng \(\left( {ABC} \right)\) là \(d = \frac{{3V}}{S}\) Lời giải chi tiết :
Diện tích tam giác ABC là \(\frac{{{a^2}\sqrt 3 }}{4}\) Khoảng cách từ \(S\) đến mặt phẳng \(\left( {ABC} \right)\) là \(d = \frac{{3V}}{{{S_{ABC}}}} = \frac{{3.\frac{{{a^3}}}{4}}}{{\frac{{{a^2}\sqrt 3 }}{4}}} = a\sqrt 3 \) Đáp án B.
Câu 25 :
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) cạnh \(a\). I là trung điểm CD'. Khoảng cách từ \(I\) dến mặt phằng \(\left( {BDD'B'} \right)\) bằng
Đáp án : A Phương pháp giải :
Đưa về khoảng cách từ C’ đến (BDD’B’) Lời giải chi tiết :
Mà \(A'C' \bot B'D' \Rightarrow A'C' \bot \left( {BDD'B'} \right)\) \(\begin{array}{*{20}{l}}{ \Rightarrow d\left( {C';\left( {BDD'B'} \right)} \right) = C'O}\\{C'O = \frac{1}{2}A'C' = \frac{1}{2}\sqrt {2{a^2}} {\rm{ \;}} = \frac{{a\sqrt 2 }}{2}}\\{ \Rightarrow d\left( {I;\left( {BDD'B'} \right)} \right) = \frac{{a\sqrt 2 }}{4}}\end{array}\) Đáp án A.
Câu 26 :
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} + x\), biết tiếp tuyến đó vuông góc với đường thẳng \(y = {\rm{ \;}} - \frac{1}{5}x + 2\).
Đáp án : B Phương pháp giải :
- Hai đường thẳng vuông góc khi và chỉ khi tích hệ số góc của chúng bằng \( - 1\). - Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\). Lời giải chi tiết :
Ta có \(y' = 4{x^3} + 1\). Hệ số góc của tiếp tuyến của đồ thị tại điểm có hoành độ \(x = {x_0}\) là \(k = 4x_0^3 + 1\). Vì tiếp tuyến vuông góc với đường thẳng \(y = {\rm{ \;}} - \frac{1}{5}x + 2\) nên \(k\left( { - \frac{1}{5}} \right) = {\rm{ \;}} - 1 \Leftrightarrow k = 5\). \( \Rightarrow 4x_0^3 + 1 = 5 \Leftrightarrow {x_0} = 1 \Rightarrow {y_0} = 2\). Vậy phương trình tiếp tuyến cần tìm là: \(y = 5\left( {x - 1} \right) + 2 = 5x - 3\). Đáp án B.
Câu 27 :
Cho khối hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có đáy là hình vuông, \(BD = 2a\), góc phẳng nhị diện \(\left[ {A',BD,A} \right]\) bằng \(30^\circ \). Tính độ dài cạnh AA'
Đáp án : D Phương pháp giải :
Xác định góc giữa hai mặt phẳng tạo thành. Lời giải chi tiết :
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AO}\\{BD \bot AA'}\end{array} \Rightarrow BC \bot \left( {A'AO} \right) \Rightarrow BD \bot A'O} \right.\). Khi đó: \(\left\{ {\begin{array}{*{20}{l}}{\left( {A'BD} \right) \cap \left( {ABD} \right) = BD}\\{A'O \bot BD}\\{AO \bot BD}\end{array}\; \Rightarrow \left[ {A',BD,A} \right] = \widehat {A'OA} = 30^\circ } \right.\). Xét vuông tại \(A\), ta có: \({\rm{tan}}\widehat {A'OA} = \frac{{AA'}}{{AO}} \Rightarrow AA' = \frac{1}{{\sqrt 3 }} \cdot a = \frac{{a\sqrt 3 }}{3}\). Đáp án D.
Câu 28 :
Kim tự tháp Kê - ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao là 147m, cạnh đáy là 230m. Thể tích của nó là
Đáp án : B Phương pháp giải :
Thể tích của khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là \(V = \frac{1}{3}Sh\) Lời giải chi tiết :
Thể tích của kim tự tháp là \(V = \frac{1}{3}{.230^2}.147 = 2592100\left( {{m^3}} \right)\) Đáp án B.
Câu 29 :
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại \(A\), góc giữa A'C với mặt đáy \(\left( {ABC} \right)\) bằng \(45^\circ \) và \(AA' = 4\). Gọi \(M\) là trung điểm của CC'. Khoảng cách từ \(M\) đến mặt phẳng \(\left( {A'BC} \right)\) bằng
Đáp án : A Phương pháp giải :
- Dựng góc giữa A'C với mặt đáy \(\left( {ABC} \right)\) bằng \({45^0}\) - \(d\left( {M,\left( {A'BC} \right)} \right) = \frac{1}{2}d\left( {C',\left( {A'BC} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A'BC} \right)} \right)\) - Tính \(d\left( {A,\left( {A'BC} \right)} \right)\) Lời giải chi tiết :
Gọi \(H\) là trung điểm của BC Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AH \bot BC\) Mà \(AA' \bot BC \Rightarrow \left( {A'AH} \right) \bot BC \Rightarrow \left( {A'AH} \right) \bot \left( {A'BC} \right)\) Kẻ \(AK \bot A'H{\mkern 1mu} {\mkern 1mu} \left( {K \in A'H} \right)\) Khi đó \(AK \bot \left( {A'BC} \right) \Rightarrow d\left( {A,\left( {A'BC} \right)} \right) = AK\) Ta có: \(\left( {A'C,\left( {ABC} \right)} \right) = \left( {A'C,AC} \right) = \widehat {A'CA}\) Theo giả thiết \(\angle A'CA = 45^\circ \Rightarrow \widehat {A'AC}\) vuông cân tại \(A\) Do đó \(AC = AA' = 4\) Khi đó \(BC = AC\sqrt 2 {\rm{ \;}} = 4\sqrt 2 {\rm{ \;}} \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{4.4}}{{4\sqrt 2 }} = 2\sqrt 2 \) Xét \(\Delta A'AH\) có \(AK \bot A'H\): \(AK = {\rm{ }}\frac{{AA'.AH}}{{\sqrt {AA{'^2} + A{H^2}} }} = \frac{{4.2\sqrt 2 }}{{\sqrt {16 + 8} }} = \frac{{4\sqrt 3 }}{3}\) \( \Rightarrow d\left( {M,\left( {A'BC} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A'BC} \right)} \right) = \frac{1}{2}.\frac{{4\sqrt 3 }}{3} = \frac{{2\sqrt 3 }}{3}\) Vậy khoảng cách từ \(M\) đến mặt phẳng \(\left( {A'BC} \right)\) bằng \(\frac{{2\sqrt 3 }}{3}\) Đáp án A.
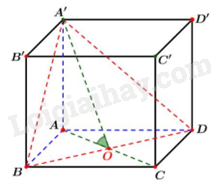
Câu 30 :
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,SA vuông góc với mặt đáy và \(SA = \frac{{a\sqrt 6 }}{6}\). Khi đó số đo của góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là
Đáp án : A Phương pháp giải :
Xác định góc giữa hai mặt phẳng tạo thành. Lời giải chi tiết :
Gọi \(O\) là tâm của hình vuông ABCD. Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AO}\\{BD \bot SA}\end{array} \Rightarrow BD \bot \left( {SAO} \right) \Rightarrow BD \bot OA} \right.\). Khi đó: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBD} \right) \cap \left( {ABD} \right) = BD}\\{OA \bot BD}\\{SO \bot BD}\end{array}\; \Rightarrow \left[ {S,BD,A} \right] = } \right.\widehat {SOA}\). Xét vuông tại \(A\), ta có: \({\rm{tan}}\widehat {SOA} = \frac{{SA}}{{OA}} = \frac{{\frac{{a\sqrt 6 }}{6}}}{{\frac{{a\sqrt 2 }}{2}}} = \frac{{\sqrt 3 }}{3} \Rightarrow \widehat {SOA} = 30^\circ \) Vậy góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) bằng \(30^\circ \). Đáp án A.
Câu 31 :
Tổng tất cả các nghiệm của phương trình \({9^x} - {4.3^x} + 3 = 0\) bằng
Đáp án : D Phương pháp giải :
Giải phương trình bậc hai đối với hàm số mũ. Lời giải chi tiết :
Ta có: \(\begin{array}{*{20}{l}}{{9^x} - {{4.3}^x} + 3 = 0 \Leftrightarrow {{\left( {{3^x}} \right)}^2} - {{4.3}^x} + 3 = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{3^x} = 1}\\{{3^x} = 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array}} \right.} \right.}\end{array}\) Vậy tổng tất cả các nghiệm của phương trình là \(0 + 1 = 1\). Đáp án D.
Câu 32 :
Trong một lớp 10 có 50 học sinh. Khi đăng ký cho học phụ đạo thì có 38 học sinh đăng ký học Toán, 30 học sinh đăng ký học Lý, 25 học sinh đăng ký học cả Toán và Lý. Nếu chọ ngẫu nhiên 1 học sinh của lớp đó thì xác suất để em này không đăng ký học phụ đạo môn nào cả là bao nhiêu
Đáp án : B Phương pháp giải :
Hai biến cố A, B bất kì ta có: \({\rm{P}}\left( {{\rm{A}} \cup {\rm{B}}} \right) = {\rm{P}}\left( {\rm{A}} \right) + {\rm{P}}\left( {\rm{B}} \right) - {\rm{P}}\left( {{\rm{A}} \cap {\rm{B}}} \right)\). Lời giải chi tiết :
Gọi A là biến cố "học sinh đăng ký Toán" Gọi B là biến cố "học sinh đăng ký Lý" \(A \cap B\) "học sinh đăng ký Toán, Lý" \({\rm{A}} \cup {\rm{B}}\) là biến cố "học sinh có đăng ký học phụ đạo" \({\rm{P}}\left( {{\rm{A}} \cup {\rm{B}}} \right) = {\rm{P}}\left( {\rm{A}} \right) + {\rm{P}}\left( {\rm{B}} \right) - {\rm{P}}\left( {{\rm{A}} \cap {\rm{B}}} \right) = \frac{{38}}{{50}} + \frac{{30}}{{50}} - \frac{{25}}{{50}} = \frac{{43}}{{50}}\) \(\overline {{\rm{A}} \cup {\rm{B}}} \) là biến cố "học sinh không đăng ký môn nào cả" \({\rm{P}}\left( {\overline {{\rm{A}} \cup {\rm{B}}} } \right) = 1 - P\left( {{\rm{A}} \cup {\rm{B}}} \right) = \frac{8}{{50}} = 0,14\) Đáp án B.
Câu 33 :
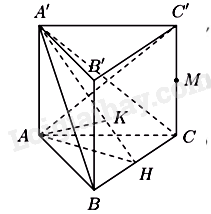
Cho khối lăng trụ \(ABC \cdot A'B'C'\) có đáy ABC là tam giác vuông cân tại \(A\), \(A'A = A'B = A'C = a\). Biết góc giữa hai mặt phẳng \(\left( {BCC'B'} \right)\) và \(\left( {ABC} \right)\) bằng \(30^\circ \), thể tích của khối lăng trụ đã cho bằng
Đáp án : C Phương pháp giải :
Gọi H là trung điểm BC, M là trung điểm của B’C’ \( \Rightarrow A'H \bot \left( {ABC} \right)\) và \(A'MH = 30^\circ \) từ đó tìm BC, AH và tính thể tích lăng trụ. Lời giải chi tiết :
Do \(A'A = A'B = A'C = a\) nên hình chiếu của A’ xuống (ABC) là trọng tâm của \(\Delta ABC\) Gọi H là trung điểm BC, M là trung điểm của B’C’
Do \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AH}\\{BC \bot A'H}\end{array}} \right. \Rightarrow BC \bot \left( {AA'H} \right) \Rightarrow BC \bot AA' \Rightarrow BC \bot HM\) \(\begin{array}{*{20}{l}}{ \Rightarrow \left( {\left( {ABC} \right),\left( {BCC'B'} \right)} \right) = \left( {\left( {A'B'C'} \right),\left( {BCC'B'} \right)} \right) = A'MH = 30^\circ }\\{ \Rightarrow A'H = HM.\sin 30^\circ = \frac{a}{2}}\\{ \Rightarrow A'M = \frac{{A'H}}{{\tan 30^\circ }} = \frac{{a\sqrt 3 }}{2} \Rightarrow BC = 2A'M = a\sqrt 3 }\\{ \Rightarrow V = A'H.\frac{1}{2}AH.BC = \frac{1}{2}.\frac{a}{2}.\frac{{a\sqrt 3 }}{2}.a\sqrt 3 {\rm{ \;}} = \frac{{3{a^3}}}{8}}\end{array}\) Đáp án C.
Câu 34 :
Tìm số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{3}}}\left( {4x - 9} \right) > {\log _{\frac{1}{3}}}\left( {x + 10} \right)\)
Đáp án : A Phương pháp giải :
\({\log _{\frac{1}{3}}}\left( {4x - 9} \right) > {\log _{\frac{1}{3}}}\left( {x + 10} \right) \Leftrightarrow 4x - 9 < x + 10\) Chú ý về điều kiện xác định của bất phương trình logarit Lời giải chi tiết :
\({\log _{\frac{1}{3}}}\left( {4x - 9} \right) > {\log _{\frac{1}{3}}}\left( {x + 10} \right)\) Đk: \(x > \frac{9}{4}\) \(\begin{array}{*{20}{l}}{ \Leftrightarrow 4x - 9 < x + 10}\\{ \Leftrightarrow 3x < 19}\\{ \Leftrightarrow x < \frac{{19}}{3}}\end{array}\) Kết hợp với ĐK ta được \(\frac{9}{4} < x < \frac{{19}}{3}\) Mà x nguyên nên \(x \in \left\{ {3,4,5,6} \right\}\) Vậy có tất cả 4 nghiệm nguyên x của bất phương trình Đáp án A.
Câu 35 :
Tìm \(m\) để hàm số \(y = \frac{{m{x^3}}}{3} - m{x^2} + \left( {3m - 1} \right)x + 1\) có \(y' \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R\)
Đáp án : C Phương pháp giải :
Tính đạo hàm của hàm số. Giải bpt \(y' \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R\) Lời giải chi tiết :
\(\begin{array}{*{20}{l}}{y = \frac{{m{x^3}}}{3} - m{x^2} + \left( {3m - 1} \right)x + 1}\\{ \Rightarrow y' = m{x^2} - 2mx + 3m - 1}\\{y' \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Rightarrow m{x^2} - 2mx + 3m - 1 \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R}\end{array}\) TH1: m = 0, khi đó \(BPT \Leftrightarrow {\rm{\;}} - 1 \le 0\) , đúng \(\forall x \in R\) TH2: \(\begin{array}{*{20}{l}}{m \ne 0 \Leftrightarrow y' \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = m < 0}\\{\Delta ' = {m^2} - m\left( {3m - 1} \right) \le 0}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 0}\\{ - 2{m^2} + m \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 0}\\{\left[ {\begin{array}{*{20}{l}}{m \le 0}\\{m \ge \frac{1}{2}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow m < 0}\end{array}\) Kết hợp cả 2 trường hợp ta có \(m \le 0\) là những giá trị cần tìm. Đáp án C.
II. Tự luận
Phương pháp giải :
Chia trường hợp và tính xác suất. Lời giải chi tiết :
Từ giả thiết suy ra xác suất để người thứ nhất, thứ hai, thứ ba bẳn không trúng đích lần lượt là 0,5;0,4 và 0,2. Để có ít nhất 2 người bẳn trúng đích thì có các trường hợp sau TH1: Người thứ nhất và người thứ hai bắn trúng, người thứ ba bắn không trúng có xác suất là:\(0,5 \times 0,6 \times 0,2 = 0,06\). TH2: Người thứ nhất và người thứ ba bắn trúng, người thứ hai bắn không trúng có xác suất là:\(0,5 \times 0,8 \times 0,4 = 0,16\). TH3: Người thứ hai và thứ ba bắn trúng, người thứ nhất bắn không trúng có xác suất là:\(0,5 \times 0,6 \times 0,8 = 0,24\) TH4: Cả ba người đều trúng đích: \(0,5 \times 0,6 \times 0,8 = 0,24\). Vậy xác suất để có ít nhất 2 người bắn trúng đích là: \(0,06 + 0,24 + 0,16 + 0,24 = 0,7\). Phương pháp giải :
Tìm tập xác định. Gọi \(M\left( {{x_0};{y_0}} \right)\) là tiếp điểm của \(\left( C \right)\) và tiếp tuyến, tính \(f'\left( {{x_o}} \right)\) Vì tiếp tuyến song song với đường thẳng \(y = 9x + 5\) nên \(f'\left( {{x_0}} \right) = 9\) nên ta tìm được các giá trị \({x_o}\). Lời giải chi tiết :
TXĐ: \(D = R\backslash \left\{ { - 4} \right\},y' = \frac{9}{{{{\left( {x + 4} \right)}^2}}}\) Gọi \(M\left( {{x_0};{y_0}} \right)\) là tiếp điểm của \(\left( C \right)\) và tiếp tuyến. Vì tiếp tuyến song song với đường thẳng \(y = 9x + 5\) nên \(f'\left( {{x_0}} \right) = 9\) \( \Leftrightarrow \frac{9}{{{{\left( {{x_0} + 4} \right)}^2}}} = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x_0} = {\rm{\;}} - 3}\\{{x_0} = {\rm{\;}} - 5}\end{array}} \right.\) \({x_0} = {\rm{\;}} - 3 \Rightarrow {y_0} = {\rm{\;}} - 7 \Rightarrow pttt:y = 9x + 20\) \({x_0} = {\rm{\;}} - 5 \Rightarrow {y_0} = 11 \Rightarrow pttt:y = 9x + 56\) Phương pháp giải :
a) \(\left\{ {\begin{array}{*{20}{l}}{d \bot \left( P \right)}\\{\left( Q \right) \supset d}\end{array}} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\). b) Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. c) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. d) Sử dụng phương pháp đổi đỉnh. Lời giải chi tiết :
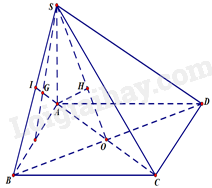
a) Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AB{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\\{BC \bot SA{\mkern 1mu} {\mkern 1mu} \left( {SA \bot \left( {ABCD} \right)} \right)}\end{array}} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\). \(\left\{ {\begin{array}{*{20}{l}}{BD \bot SA{\mkern 1mu} {\mkern 1mu} \left( {SA \bot \left( {ABCD} \right)} \right)}\\{BD \bot AC{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {gt} \right)}\end{array}} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {SBD} \right) \bot \left( {SAC} \right)\). b) Ta có \(BC \bot \left( {SAB} \right){\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {\left( {SC;SB} \right)} = \widehat {CSB}\). Trong tam giác SBC vuông tại \(B\) ta có : \(\begin{array}{*{20}{l}}{SB = \sqrt {S{A^2} + A{B^2}} {\rm{\;}} = \sqrt {12{a^2} + 4{a^2}} {\rm{\;}} = 4a}\\{BC = 2a \Rightarrow \tan \widehat {CSB} = \frac{{BC}}{{SB}} = \frac{1}{2} \Rightarrow \widehat {CSB} \approx 26^\circ 34'}\end{array}\) Vậy \(\widehat {\left( {SC;\left( {SAB} \right)} \right)} \approx 26^\circ 34'\). c) Gọi \(O = AC \cap BD\). Ta có: \(BD \bot \left( {SAC} \right){\mkern 1mu} {\mkern 1mu} \left( {cmt} \right) \Rightarrow BD \bot SO\). \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBD} \right) \cap \left( {ABCD} \right) = BD}\\{\left( {SBD} \right) \supset SO \bot BD}\\{\left( {ABCD} \right) \supset AO \bot BD}\end{array}} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SO;AO} \right)} = \widehat {SOA}\). ABCD là hình vuông cạnh \(2a \Rightarrow AC = BD = 2a\sqrt 2 {\rm{\;}} \Rightarrow AO = \frac{1}{2}AC = a\sqrt 2 \). Trong tam giác vuông SAO ta có : \(SO = \sqrt {S{A^2} + A{O^2}} {\rm{\;}} = \sqrt {12{a^2} + 2{a^2}} {\rm{\;}} = a\sqrt {14} \). \( \Rightarrow \tan \widehat {SOA} = \frac{{SA}}{{AO}} = \frac{{a\sqrt {14} }}{{a\sqrt 2 }} = \sqrt 7 {\rm{\;}} \Rightarrow \widehat {SOA} \approx 69^\circ 18'\). Vậy \(\widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} \approx 69^\circ 18'\). d) Trong \(\left( {SAO} \right)\) kẻ \(AH \bot SO{\mkern 1mu} {\mkern 1mu} \left( {H \in SO} \right)\). Ta có \(BD \bot \left( {SAC} \right) \Rightarrow BD \bot AH\). \(\left\{ {\begin{array}{*{20}{l}}{AH \bot BD}\\{AH \bot SO}\end{array}} \right. \Rightarrow AH \bot \left( {SBD} \right) \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AH\). Áp dụng hệ thức lượng trong tam giác vuông SOA ta có: \(AH = \frac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \frac{{2a\sqrt 3 .a\sqrt 2 }}{{\sqrt {12{a^2} + 2{a^2}} }} = \frac{{2\sqrt {21} a}}{7}\). Vậy \(d\left( {A;\left( {SBD} \right)} \right) = \frac{{2\sqrt {21} a}}{7}\). Trong \(\left( {SAB} \right)\), gọi \(I = AG \cap SB\) ta có: \(AG \cap \left( {SBD} \right) = I\). \( \Rightarrow \frac{{d\left( {G;\left( {SBD} \right)} \right)}}{{d\left( {A;\left( {SBD} \right)} \right)}} = \frac{{GI}}{{AI}} = \frac{1}{3} \Rightarrow d\left( {G;\left( {SBD} \right)} \right) = \frac{1}{3}d\left( {A;\left( {SBD} \right)} \right) = \frac{{2\sqrt {21} a}}{{21}}\).
|






















Danh sách bình luận