Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 4Tải về Câu 1: Góc có số đo \(250^\circ \) thì có số đo theo đơn vị là radian là: Quảng cáo
Đề bài Phần trắc nghiệm (4 điểm) Câu 1: Góc có số đo \(250^\circ \) thì có số đo theo đơn vị là radian là:
Câu 2: Tính \(P = \sin \left( {\alpha + \frac{\pi }{2}} \right) + \cos \left( {3\pi - \alpha } \right) + \cot \left( {\pi - \alpha } \right)\), biết \(\sin \alpha = - \frac{1}{2}\) và \( - \frac{\pi }{2} < \alpha < 0\).
Câu 3: Giá trị của biểu thức \(A = \sin \left( {\frac{\pi }{3} + \frac{\pi }{4}} \right)\) là:
Câu 4: Công thức \(\sin 2a\) bằng
Câu 5: Chu kỳ tuần hoàn của hàm số \(y = \sin x\) là
Câu 6: Hàm số nào sau đây là hàm số lẻ?
Câu 7: Tập nghiệm của phương trình \(\cos x = - 1\) là:
Câu 8: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình \(\sin \left( {3x - \frac{{3\pi }}{4}} \right) = \frac{{\sqrt 3 }}{2}\) bằng:
Câu 9: Cho dãy số \(1,\,\frac{1}{3},\,\frac{1}{9},\,\frac{1}{{27}},\,...\) (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng quát của dãy số đã cho là
Câu 10: Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \({u_n} = 2n - 1\) với \(n \ge 1\). Số hạng \({u_1}\) bằng
Câu 11: Trong các dãy số \(\left( {{u_n}} \right)\) sau đây, dãy số nào là cấp số cộng?
Câu 12: Cho cấp số cộng \(\left( {{u_n}} \right)\)biết \({u_6} = 48\) và \({u_{11}} = 83\). Tìm cặp \(\left( {{u_1};{\rm{ }}d} \right)\).
Câu 13: Trong hội chợ, một công ty sơn muốn xếp \(1089\) hộp sơn theo số lượng \(1\,,\,3\,,5\,,\,...\) từ trên xuống dưới. Hàng cuối cùng có bao nhiêu hộp sơn?
Câu 14: Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân?
Câu 15: Một cấp số nhân có số hạng đầu \({u_1} = 3\), công bội \(q = 2\). Biết \({S_n} = 765\). Tìm \(n\)?
Câu 16: Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là \(\frac{1}{2}\), số hạng thứ tư là \(32\) và số hạng cuối là \(2048\)?
Câu 17: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau:
Giá trị đại diện của nhóm thứ tư là
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là
Câu 19: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Tứ phân vị thứ nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm này là
Câu 20: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là
Phần tự luận (6 điểm) Bài 1. (1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = {\tan ^2}x - \tan x + 1\) với \(x \in \left[ { - \frac{\pi }{4};\,\frac{\pi }{4}} \right]\). Bài 2. (1,5 điểm) a) Giải phương trình \(cot\left( {x + \frac{\pi }{3}} \right) = \sqrt 3 \) b) Giải phương trình \(\cos 3x - \sin 2x = 0\) c) Giải phương trình \(\sin 4x + 1 - 2\cos 2x = \sin 2x\). Bài 3. (2 điểm) a) Cho cấp số cộng \(\left\{ {{u_n}} \right\}\) có \({u_4} = - 12\); \({u_{14}} = 18\). Tổng của 16 số hạng đầu tiên của cấp số cộng bằng bao nhiêu ? b) Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt \(20000\) đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước. Người đó thua \(9\) lần liên tiếp và thắng ở lần thứ \(10.\) Hỏi du khác trên thắng hay thua bao nhiêu? Bài 4. (1,5 điểm) Một cửa hàng đã ghi lại số tiền bán xăng cho 35 khách hàng đi xe máy. Mẫu số liệu gốc có dạng: \({x_1},{x_2}, \ldots ,{x_{35}}\) trong đó \({x_i}\) là số tiền bán xăng cho khách hàng thứ \(i\). Vì một lí do nào đó, cửa hàng chỉ có mẫu số liệu ghép nhóm dạng sau:
a) Tính trung vị của mẫu số liệu ghép nhóm này. b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này.
-------- Hết -------- Lời giải chi tiết Phần trắc nghiệm (4 điểm)
Câu 1: Trên đường tròn lượng giác, cho góc lượng giác có số đo \(\frac{\pi }{2}\) thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác trên đều có số đo dạng
Phương pháp Nếu một góc lượng giác có số đo \({\alpha ^o}\)(hay \(\alpha \)radian) thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác đó có dạng \({\alpha ^o} + k{360^o}\)(hoặc \(\alpha + k2\pi \)) với k là số nguyên. Lời giải Trên đường tròn lượng giác, mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác có số đo \(\frac{\pi }{2}\) thì đều có số đo dạng \(\frac{\pi }{2} + k2\pi ,\left( {k \in \mathbb{Z}} \right)\). Đáp án C Câu 2: Tính \(P = \sin \left( {\alpha + \frac{\pi }{2}} \right) + \cos \left( {3\pi - \alpha } \right) + \cot \left( {\pi - \alpha } \right)\), biết \(\sin \alpha = - \frac{1}{2}\) và \( - \frac{\pi }{2} < \alpha < 0\).
Phương pháp B1: Biến đổi biểu thức P để chỉ còn các giá trị lượng giác của góc \(\alpha \) B2: Từ \(\sin \alpha = - \frac{1}{2}\) và \( - \frac{\pi }{2} < \alpha < 0\) tính các giá trị lượng giác còn lại của góc \(\alpha \) Lời giải Ta có : \(P = \sin \left( {\alpha + \frac{\pi }{2}} \right) + \cos \left( {3\pi - \alpha } \right) + \cot \left( {\pi - \alpha } \right)\) \( = \sin \left( {\frac{\pi }{2} - \left( { - \alpha } \right)} \right) + \cos \left( {2\pi + \pi - 2\alpha } \right) + \cot \left( {\pi - \alpha } \right)\) \( = \cos \left( { - \alpha } \right) - \cos \left( { - \alpha } \right) + \cot \left( { - \alpha } \right)\). \( = \cos \alpha - \cos \alpha - \cot \alpha \) \( = - \cot \alpha \). Do \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{1}{2}} \right)^2} = \frac{3}{4} \Rightarrow \cos \alpha = \pm \frac{{\sqrt 3 }}{2}\) . Mà \( - \frac{\pi }{2} < \alpha < 0 \Rightarrow \cos \alpha > 0\) nên \(\cos \alpha = \frac{{\sqrt 3 }}{2}\). Suy ra \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = - \sqrt 3 \). Do đó \(P = - \cot \alpha = \sqrt 3 \) .
Đáp án C Câu 3: Giá trị của biểu thức \(A = \sin \left( {\frac{\pi }{3} + \frac{\pi }{4}} \right)\) là:
Phương pháp Sử dụng công thức cộng. Lời giải Ta có \(A = \sin \left( {\frac{\pi }{3} + \frac{\pi }{4}} \right) = \sin \frac{\pi }{3}\cos \frac{\pi }{4} + \sin \frac{\pi }{4}\cos \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}.\) Đáp án B Câu 4: Công thức \(\sin 2a\) bằng
Phương pháp Áp dụng công thức nhân đôi Lời giải Ta có: \(\sin 2a = 2\sin a.\cos a\). Đáp án A Câu 5: Chu kỳ tuần hoàn của hàm số \(y = \sin x\) là
Phương pháp Tính tuần hoàn của hàm số lượng giác cơ bản: - Hàm số \(y = \sin x\) tuần hoàn với chu kì \(T = 2\pi \). - Hàm số \(y = \cos x\) tuần hoàn với chu kì \(T = 2\pi \). - Hàm số \(y = \tan x\) tuần hoàn với chu kì \(T = \pi \). - Hàm số \(y = \cot x\) tuần hoàn với chu kì \(T = \pi \). Lời giải Hàm số \(y = \sin x\) tuần hoàn với chu kì \(T = 2\pi \). Đáp án D Câu 6: Hàm số nào sau đây là hàm số lẻ?
Phương pháp Bước 1: Tìm tập xác định \(D\) của hàm số, khi đó: - Nếu \(D\) là tập đối xứng (tức \(\forall x \in D \Rightarrow - x \in D\)), thì ta thực hiện tiếp bước 2. - Nếu \(D\) không phải tập đối xứng (tức là \(\exists x \in D\) mà \( - x \notin D\)) thì ta kết luận hàm số không chẵn không lẻ. Bước 2: Xác định \(f\left( { - x} \right)\): - Nếu \(f\left( { - x} \right) = f\left( x \right),\forall x \in D\) thì kết luận hàm số là hàm số chẵn. - Nếu \(f\left( { - x} \right) = - f\left( x \right),\forall x \in D\) thì kết luận hàm số là hàm số lẻ. - Nếu không thỏa mãn một trong hai điều kiện trên thì kết luận hàm số không chẵn không lẻ. Lời giải Tập xác định của hàm số\(y = f\left( x \right) = - 2\sin x\) là \(D = \mathbb{R}\). Do đó, nếu \(x\) thuộc tập xác định \(D\) thì \( - x\)cũng thuộc tập xác định \(D\). Ta có \(f\left( { - x} \right) = - 2\sin ( - x) = \sin x = - f\left( x \right)\). Vậy \(y = - 2\sin x\) là hàm số lẻ. Đáp án C Câu 7: Tập nghiệm của phương trình \(\cos x = - 1\) là:
Phương pháp - Trường hợp \(\left| m \right| > 1\) phương trình vô nghiệm. - Trường hợp \(\left| m \right| \le 1\), khi đó: Tồn tại duy nhất một số thực \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\cos \alpha = m\). Ta có : \(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.,\left( {k \in \mathbb{Z}} \right)\). Lời giải Ta có \(\cos x = - 1 \Leftrightarrow x = \pi + k2\pi ,k \in \mathbb{Z}\). Đáp án D Câu 8: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình \(\sin \left( {3x - \frac{{3\pi }}{4}} \right) = \frac{{\sqrt 3 }}{2}\) bằng:
Phương pháp Áp dụng các công thức giải phương trình lượng giác cơ bản rồi kết hợp điều kiện đã cho để chọn nghiệm thỏa mãn. Lời giải Ta có \(\sin \left( {3x - \frac{{3\pi }}{4}} \right) = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {3x - \frac{{3\pi }}{4}} \right) = \sin \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}3x - \frac{{3\pi }}{4} = \frac{\pi }{3} + k2\pi \\3x - \frac{{3\pi }}{4} = \pi - \frac{\pi }{3} + k2\pi \end{array} \right.\).\( \Leftrightarrow \left[ \begin{array}{l}3x = \frac{{13\pi }}{{12}} + k2\pi \\3x = \frac{{17\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{13\pi }}{{36}} + k\frac{{2\pi }}{3}\\x = \frac{{17\pi }}{{36}} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in Z} \right).\) TH1. Với TH2. Với So sánh bốn nghiệm ta được nghiệm âm lớn nhất là \(x = - \frac{{7\pi }}{{36}}\) và nghiệm dương nhỏ nhất là \(x = \frac{{13\pi }}{{36}}.\) Khi đó tổng hai nghiệm bằng \(\frac{{13\pi }}{{36}} - \frac{{7\pi }}{{36}} = \frac{\pi }{6}.\) Đáp án C Câu 9: Cho dãy số \(1,\,\frac{1}{3},\,\frac{1}{9},\,\frac{1}{{27}},\,...\) (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng quát của dãy số đã cho là
Phương pháp Tìm tính chất chung của các số trong dãy số rồi dự đoán công thức tổng quát. Lời giải Từ các số hạng đầu tiên của dãy số ta dự đoán \({u_n} = {\left( {\frac{1}{3}} \right)^{n - 1}}\). Đáp án C Câu 10: Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \({u_n} = 2n - 1\) với \(n \ge 1\). Số hạng \({u_1}\) bằng
Phương pháp Thay \(n = 1\) vào công thức tổng quát của dãy số. Lời giải Ta có: \({u_1} = 2.1 - 1 = 1\) Đáp án A Câu 11: Trong các dãy số \(\left( {{u_n}} \right)\) sau đây, dãy số nào là cấp số cộng?
Phương pháp Để chứng minh dãy số \(\left( {{u_n}} \right)\) là một cấp số cộng, ta xét \(A = {u_{n + 1}} - {u_n}\) \( \bullet \) Nếu \(A\) là hằng số thì \(\left( {{u_n}} \right)\) là một cấp số cộng với công sai \(d = A\). \( \bullet \) Nếu \(A\) phụ thuộc vào \(n\) thì \(\left( {{u_n}} \right)\) không là cấp số cộng. Lời giải Xét phương án A: \({u_2} = 7,\,{u_3} = 15\) vì \({u_2} - {u_1} \ne \,{u_3} - {u_2}\) do đó \(\left( {{u_n}} \right)\) không phải là cấp số cộng. Xét phương án B: theo giả thiết ta có \({u_{n + 1}} - {u_n} = 2,\,\forall n \in {\mathbb{N}^ * }\) do đó \(\left( {{u_n}} \right)\) là cấp số cộng. Xét phương án C: \({u_2} = 0,\,{u_3} = - 1,\,{u_4} = - 2;\,{u_5} = - 9\) do đó \(\left( {{u_n}} \right)\) không phải là cấp số cộng. Xét phương án D: \({u_2} = 2,\,{u_3} = 4\) vì \({u_2} - {u_1} \ne \,{u_3} - {u_2}\) do đó \(\left( {{u_n}} \right)\) không phải là cấp số cộng. Đáp án B Câu 12: Cho cấp số cộng \(\left( {{u_n}} \right)\)biết \({u_6} = 48\) và \({u_{11}} = 83\). Tìm cặp \(\left( {{u_1};{\rm{ }}d} \right)\).
Phương pháp Dựa vào giả thuyết, ta lập một hệ phương trình chứa công sai d và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được d và \({u_1}\). Lời giải Ta có: \(\left\{ \begin{array}{l}{u_6} = 48\\{u_{11}} = 83\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} + 5d = 48\\{u_1} + 10d = 83\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 13\\d = 7\end{array} \right.\). Đáp án C Câu 13: Trong hội chợ, một công ty sơn muốn xếp \(1089\) hộp sơn theo số lượng \(1\,,\,3\,,5\,,\,...\) từ trên xuống dưới. Hàng cuối cùng có bao nhiêu hộp sơn?
Phương pháp Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai \(d\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\) hoặc \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d\) . Lời giải Giả sử \(1089\) được xếp thành \(n\) hàng. Từ giả thiết ta có số hộp sơn trên mỗi hàng là số hạng của một cấp số cộng \(\left( {{u_n}} \right)\) với số hạng đầu \({u_1} = 1\) công sai \(d = 2\). Do đó: \({S_n} = 1089 \Leftrightarrow n + n\left( {n - 1} \right) = 1089 \Leftrightarrow n = 33\). Vậy số hộp sơn ở hàng cuối cùng là: \({u_{33}} = 1 + 32.2 = 65\). Đáp án B Câu 14: Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân?
Phương pháp Chứng minh \(\forall n \ge 1,{u_{n + 1}} = {u_n}.q\) trong đó \(q\) là một số không đổi. Nếu \({u_n} \ne 0\) với mọi \(n \in {\mathbb{N}^*}\) thì ta lập tỉ số \(T = \frac{{{u_{n + 1}}}}{{{u_n}}}\). \( * \) T là hằng số thì \(({u_n})\) là cấp số nhân có công bội \(q = T\). \( * \) T phụ thuộc vào n thì \(({u_n})\) không là cấp số nhân. Lời giải Ta thấy ở đáp án C có \(6 = 3.2\), \(12 = 6.2\), \(24 = 12.2\) nên đây là cấp số nhân với công bội \(q = 2\). Đáp án C Câu 15: Một cấp số nhân có số hạng đầu \({u_1} = 3\), công bội \(q = 2\). Biết \({S_n} = 765\). Tìm \(n\)?
Phương pháp Cho một cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}},q \ne 1\). Lời giải Áp dụng công thức của cấp số nhân ta có: \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}} = \frac{{3.\left( {1 - {2^n}} \right)}}{{1 - 2}} = 765\)\( \Leftrightarrow n = 8\). Đáp án A Câu 16: Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là \(\frac{1}{2}\), số hạng thứ tư là \(32\) và số hạng cuối là \(2048\)?
Phương pháp Cho một cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}},q \ne 1\). Lời giải Theo bài ra ta có \({u_1} = \frac{1}{2}\), \({u_4} = 32\) và \({u_n} = 2048\). \({u_4} = {u_1}.{q^3}\) \( \Rightarrow 32 = \frac{1}{2}.{q^3}\)\( \Rightarrow q = 4\) \({u_n} = 2048\)\( \Rightarrow {u_1}.\,{q^{n - 1}} = 2048\)\( \Rightarrow {4^{n - 1}} = {4^6}\)\( \Rightarrow n = 7\) Khi đó tổng của cấp số nhân này là \({S_7} = \frac{{{u_1}\left( {1 - {q^7}} \right)}}{{1 - q}} = \frac{{\frac{1}{2}\left( {1 - {4^7}} \right)}}{{1 - 4}} = \frac{{5461}}{2}\). Đáp án C Câu 17: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau:
Giá trị đại diện của nhóm thứ tư là
Phương pháp Đọc bảng số liệu. Lời giải Giá trị đại diện của nhóm thứ tư là \(\frac{{156 + 158}}{2} = 157\). Đáp án B Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là
Phương pháp Nhóm chứa mốt là nhóm có tần số lớn nhất. Lời giải Mốt \({M_0}\) chứa trong nhóm \([40;60)\) Đáp án A Câu 19: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Tứ phân vị thứ nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm này là
Phương pháp Để tính tứ phân vị thứ nhất \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\), giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó, \({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\) trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). Lời giải Cỡ mẫu là \(n = 128\). Tứ phân vị thứ nhất \({Q_1}\) là \(\frac{{{x_{32}} + {x_{33}}}}{2}\). Do \({x_{32}},{x_{33}}\) đều thuộc nhóm \([25;30)\) nên nhóm này chứa \({Q_1}\). Do đó, \(p = 3;{a_3} = 25;{m_3} = 25;{m_1} + {m_2} = 21,{a_4} - {a_3} = 5\) và ta có \({Q_1} = 25 + \frac{{\frac{{128}}{4} - 21}}{{25}} \cdot 5 = \frac{{136}}{5}\) Với tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{96}} + {x_{97}}}}{2}\). Do \({x_{96}},{x_{97}}\) đều thuộc nhóm \([35;40)\) nên nhóm này chứa \({Q_3}\). Do đó, \(p = 5;{a_5} = 35;{m_5} = 21;{m_1} + {m_2} + {m_3} + {m_4} = 7 + 14 + 25 + 37 = 83;{a_6} - {a_5} = 5\) và ta có \({Q_3} = 35 + \frac{{\frac{{3.128}}{4} - 83}}{{21}} \cdot 5 = \frac{{800}}{{21}}\). Đáp án D Câu 20: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là
Phương pháp Nhóm chứa trung vị là nhóm chứa 2 phần tử ở giữa của dãy số liệu. Lời giải Ta có: \(n = 42\) Nên trung vị của mẫu số liệu trên là \({Q_2} = \frac{{{x_{21}} + {x_{22}}}}{2}\) Mà \({x_{21}},{x_{22}} \in \left[ {40;60} \right)\) Vậy nhóm chứa trung vị của mẫu số liệu trên là nhóm \([40;60)\) Đáp án A
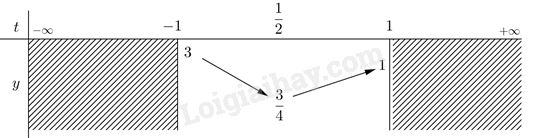
Phần tự luận. Bài 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = {\tan ^2}x - \tan x + 1\) với \(x \in \left[ { - \frac{\pi }{4};\,\frac{\pi }{4}} \right]\). Phương pháp B1: Đặt ẩn phụ và tìm điều kiện của ẩn B2: Lập bảng biến thiên, khảo sát hàm số rồi kết luận Lời giải Đặt \(tanx = t\), \(t \in \left[ { - 1\,;\,1} \right]\), hàm số có dạng: \(y = {t^2} - t + 1\). Xét hàm số \(y = {t^2} - t + 1\) trên \(\left[ { - 1\,;\,1} \right]\) có BBT như sau:
Giá trị nhỏ nhất của hàm số bằng \(\frac{3}{4}\) khi và chỉ khi \(t = \frac{1}{2}\) tức \(tanx = \frac{1}{2}\)\( \Leftrightarrow \)\(x = \arctan \left( {\frac{1}{2}} \right) + k\pi \), \(k \in \mathbb{Z}\). Giá trị lớn nhất của hàm số bằng \(3\) khi và chỉ khi \(t = - 1\) tức là \(tanx = - 1\)\( \Leftrightarrow \)\(x = - \frac{\pi }{4} + k\pi \), \(k \in \mathbb{Z}\). Bài 2. a) Giải phương trình \(cot\left( {x + \frac{\pi }{3}} \right) = \sqrt 3 \) b) Giải phương trình \(\cos 3x - \sin 2x = 0\) c) Giải phương trình \(\sin 4x + 1 - 2\cos 2x = \sin 2x\). Phương pháp a) Ta có: \(\cot x = m\,\)\( \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). b) Áp dụng các công thức lượng giác đặc biệt để đưa về phương trình lượng giác cơ bản. c) Sử dụng công thức nhân đôi để làm xuất hiện nhân tử chung: \(\sin 2x = 2\sin x\cos x\). Lời giải a) Ta có: \(cot\left( {x + \frac{\pi }{3}} \right) = \sqrt 3 \Leftrightarrow x + \frac{\pi }{3} = \frac{\pi }{6} + k\pi \)\( \Leftrightarrow x = - \frac{\pi }{6} + k\pi \) \((k \in \mathbb{Z})\). b) Ta có \({\rm{cos3}}x - \sin 2x = 0 \Leftrightarrow {\rm{cos3}}x = \sin 2x \Leftrightarrow {\rm{cos3}}x = {\rm{cos}}\left( {\frac{\pi }{2} - 2x} \right)\) \( \Leftrightarrow 3x = \pm \left( {\frac{\pi }{2} - 2x} \right) + k2\pi \), \(k \in \mathbb{Z}\). \( \Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} + k2\pi \\x = - \frac{\pi }{2} + k2\pi \end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{10}} + k\frac{{2\pi }}{5}\\x = - \frac{\pi }{2} + k2\pi \end{array} \right.(k \in \mathbb{Z})\) c) Ta có: \(\sin 4x + 1 - 2\cos 2x = \sin 2x\) \( \Leftrightarrow 2\sin 2x.\cos 2x + 1 - 2\cos 2x - \sin 2x = 0\) \( \Leftrightarrow \left( {{\rm{sin2x - 1}}} \right)\left( {2\cos 2x - 1} \right) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 2x = 1}\\{{\rm{cos2x = }}\frac{1}{2}}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k\pi }\\{{\rm{x = }}\frac{\pi }{6} + k\pi }\end{array}\quad \left( {k \in \mathbb{Z}} \right)} \right..\) Bài 3. a) Cho cấp số cộng \(\left\{ {{u_n}} \right\}\) có \({u_4} = - 12\); \({u_{14}} = 18\). Tổng của 16 số hạng đầu tiên của cấp số cộng bằng bao nhiêu ? b) Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt \(20000\) đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước. Người đó thua \(9\) lần liên tiếp và thắng ở lần thứ \(10.\) Hỏi du khác trên thắng hay thua bao nhiêu? Phương pháp a) Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai \(d\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\) hoặc \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d\) . b) Cho một cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó : \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}},q \ne 1\). Lời giải a) Ta có : \(\left\{ \begin{array}{l}{u_4} = - 12\\{u_{14}} = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + 3d = - 12\\{u_1} + 13d = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = - 21\\d = 3\end{array} \right.\). Tổng của 16 số hạng đầu tiên của cấp số cộng là: \({S_{16}} = 16.\left( { - 21} \right) + \frac{{16.15}}{2}.3 = 24\). b) Số tiền du khác đặt trong mỗi lần (kể từ lần đầu) là một cấp số nhân có \({u_1} = 20\,\,000\) và công bội \(q = 2.\) Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là: \({S_9} = {u_1} + {u_2} + ... + {u_9} = \frac{{{u_1}\left( {1 - {p^9}} \right)}}{{1 - p}} = 10220000\) Số tiền mà du khách thắng trong lần thứ \(10\) là \({u_{10}} = {u_1}.{p^9} = 10240000\) Ta có \({u_{10}} - {S_9} = 20\,\,000 > 0\) nên du khách thắng 20 000. Bài 4. Một cửa hàng đã ghi lại số tiền bán xăng cho 35 khách hàng đi xe máy. Mẫu số liệu gốc có dạng: \({x_1},{x_2}, \ldots ,{x_{35}}\) trong đó \({x_i}\) là số tiền bán xăng cho khách hàng thứ \(i\). Vì một lí do nào đó, cửa hàng chỉ có mẫu số liệu ghép nhóm dạng sau:
a) Tính trung vị của mẫu số liệu ghép nhóm này. b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này. Phương pháp a) Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau: Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Bước 2. Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right)\), trong đó \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\). Với \(p = 1\), ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). b) Để tính tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó, \({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\) trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). Để tịnh tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\). Giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó, \({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\) trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\). Tứ phân vị thứ hai \({Q_2}\) chính là trung vị \({M_e}\). Nhận xét. Ta cũng có thể xác định nhóm chứa tứ phân vi thứ \(r\) nhờ tính chất: có khoảng \(\left( {\frac{{r \cdot n}}{4}} \right)\) giá trị nhỏ hơn tứ phân vị này. Lời giải a) Trung vị là \({x_{18}}\) thuộc nhóm [30;60), do đó \(p = 2;{a_2} = 30;{m_2} = 15;{m_1} = 3,{a_3} - {a_2} = 30\) và ta có: \({M_e} = 30 + \frac{{\frac{{35}}{2} - 3}}{{15}} \times 30 = 59\) b) Tứ phân vị thứ nhất \({Q_1}\) là \({x_9}\) thuộc nhóm [30;60), do đó \(p = 2;{a_2} = 30;{m_2} = 15;{m_1} = 3;{a_3} - {a_2} = 30\) và ta có: \({Q_1} = 30 + \frac{{\frac{{35}}{4} - 3}}{{15}} \times 30 = 41.5\) Tứ phân vị thứ ba \({Q_3}\) là \({x_{27}}\) thuộc nhóm [60;90), do đó \(p = 3;{a_3} = 60;{m_3} = 10;{m_1} + {m_2} = 3 + 15 = 18;{a_4} - {a_3} = 30\) và ta có: \({Q_3} = 30 + \frac{{\frac{{3 \times 35}}{4} - 18}}{{10}} \times 30 = 54.75\)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
























Danh sách bình luận