Đề thi học kì 2 Toán 11 - Đề số 6Tổng hợp đề thi giữa kì 2 lớp 11 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.Đề bài
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Cho số thực \(x > 0\), biểu thức \(\sqrt[3]{{{x^2}\sqrt x }}\) bằng
Câu 2 :
Đạo hàm của hàm số \(f\left( x \right) = {\log _2}\left( {{x^2} + 1} \right)\) là
Câu 3 :
Tính đạo hàm của hàm số \(y = \frac{{x + 6}}{{x + 9}}\):
Câu 4 :
Tập nghiệm của phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 7} \right) = 2\) là
Câu 5 :
Giải phương trình \(f''\left( x \right) = 0\), biết \(f\left( x \right) = {x^3} - 3{x^2}\).
Câu 6 :
Đạo hàm của hàm số \(y = 2{{\rm{x}}^2} - 3{\rm{x}} + 7\) là:
Câu 7 :
Cho A,B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
Câu 8 :
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và \(OA = OB = OC = a\). Thể tích của khối tứ diện OABC bằng
Câu 9 :
Tập nghiệm của bất phương trình \(\frac{1}{{{2^x}}} > 8\) là
Câu 10 :
Cho hình chóp S.ABC có đáy ABC vuông cân tại B,\(AB = BC = a,SA = a\sqrt 3 ,\)\(SA \bot \left( {ABC} \right)\). Số đo của góc phẳng nhị diện \(\left[ {S,BC,A} \right]\) là
Câu 11 :
Hàm số \(y = {\cos ^2}3x\) có đạo hàm là
Câu 12 :
Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là \(\frac{1}{5}\) và \(\frac{2}{7}\). Gọi \(A\) là biến cố: "Cả hai cùng ném bóng trúng vào rổ". Khi đó, xác suất của biến cố \(A\) là bao nhiêu?
Câu 13 :
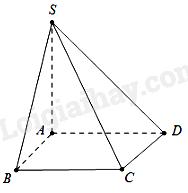
Cho hình chóp SABCD có đáy là hình chữ nhật với \(AB = a,AD = 2a\). Biết \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt {15} \). Tính góc giữa SC và mặt phẳng \(\left( {ABCD} \right)\).
Câu 14 :
Tìm tọa độ tiếp điểm của các tiếp tuyến \(\Delta \) với đồ thị của hàm số \(y = \frac{{x - 1}}{{x + 1}}\), biết tiếp tuyến đó song song với đường thẳng \(2x - y - 1 = 0\).
Câu 15 :
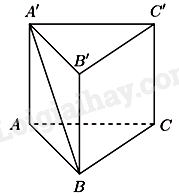
Cho khối lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng \(a\) và đường thẳng A'B hợp với mặt đáy một góc \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ ABC.A'B'C'.
Câu 16 :
Cho khối chóp có diện tích đáy bằng \(7{a^2}\) và chiều cao bằng 9a. Thể tích của khối chóp đã cho bằng
II. Trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 3. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Hai xạ A và B cùng bắn vào một mục tiêu. Xác suất trúng mục tiêu của xạ thủ thứ nhất là 0,7 . Xác suất trúng mục tiêu của xạ thủ thứ hai là 0,8 . Gọi A là biến cố: “xạ thủ thứ nhất bắn trúng”, B là biến cố: “xạ thủ thứ hai bắn trúng” Các Khẳng định dưới đây đúng hay sai? a) Khi đó \(A \cup B\) là biến cố: “Cả hai xạ thủ đều bắn trúng”
Đúng
Sai
b) Biến cố \(A \cup B\) và \(A \cap B\) là hai biến cố xung khắc
Đúng
Sai
c) Xác suất để cả hai người bắn trượt là: 0,6
Đúng
Sai
d) Xác suất để có ít nhất một người bắn trúng đích là: 0,94.
Đúng
Sai
Câu 2 :
Cho khối chóp đều \(S \cdot ABCD\) có cạnh đáy là \(a\), các mặt bên tạo với đáy một góc \(60^\circ \), O là tâm đáy. Khẳng định sau đây đúng hay sai? a) Thể tích hình chóp là: \(\frac{{{a^3}\sqrt 3 }}{2}\)
Đúng
Sai
b) Độ dài cạnh bên của hình chóp là: \(\frac{{a\sqrt 5 }}{2}\)
Đúng
Sai
c) Khoảng cách \(d\left( {O;\left( {SCB} \right)} \right)\) bằng: \(\frac{{a\sqrt 3 }}{4}\)
Đúng
Sai
d) Khoảng cách \(d\left( {AD;SC} \right) = \frac{{a\sqrt 3 }}{3}\)
Đúng
Sai
Câu 3 :
Cho hàm số \(f(x) = - \frac{m}{3}{x^3} + m{x^2} - 3x + 9\), \(g\left( x \right) = 2{x^3} - 6x + 1\) a) Phương trình tiếp tuyến của hàm \(g\left( x \right)\) tại \(x = 3\) là: \(y = 3x + 107\)
Đúng
Sai
b) Phương trình tiếp tuyến của \(g\left( x \right)\) song song với đường thẳng \(y = - 6x - 5\) là: \(y = - 6x + 1\)
Đúng
Sai
c) Phương trình \(f'\left( x \right) = g'\left( x \right)\) có hai nghiệm phân biệt với mọi \(m \in \mathbb{R}\)
Đúng
Sai
d) Để \(f'(x) \le 0\forall x \in \mathbb{R}\) thì \(m\).
Đúng
Sai
III. Tự luận trả lời ngắn
Lời giải và đáp án
I. Trắc nghiệm
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1 :
Cho số thực \(x > 0\), biểu thức \(\sqrt[3]{{{x^2}\sqrt x }}\) bằng
Câu 2 :
Đạo hàm của hàm số \(f\left( x \right) = {\log _2}\left( {{x^2} + 1} \right)\) là
Đáp án : C Phương pháp giải :
Đạo hàm của hàm số logarit Lời giải chi tiết :
Ta có: \(f'\left( x \right) = \frac{{2x}}{{\left( {{x^2} + 1} \right)\ln 2}}\) Đáp án C.
Câu 3 :
Tính đạo hàm của hàm số \(y = \frac{{x + 6}}{{x + 9}}\):
Đáp án : C Phương pháp giải :
Sử dụng công thức \({\left( {\frac{u}{v}} \right)'} = \frac{{u'v - uv'}}{{{v^2}}}\). Lời giải chi tiết :
Ta có: \(y' = \frac{{\left( {x + 9} \right) - \left( {x + 6} \right)}}{{{{\left( {x + 9} \right)}^2}}} = \frac{3}{{{{\left( {x + 9} \right)}^2}}}\). Đáp án C.
Câu 4 :
Tập nghiệm của phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 7} \right) = 2\) là
Đáp án : A Phương pháp giải :
\({\log _a}x = b \Leftrightarrow x = {a^b}\) Lời giải chi tiết :
\(\begin{array}{*{20}{l}}{{\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 7} \right) = 2 \Leftrightarrow {x^2} - 7 = {3^2}}\\{ \Leftrightarrow {x^2} - 7 = 9}\\{ \Leftrightarrow {x^2} = 16}\\{ \Leftrightarrow x = {\rm{ \;}} \pm 4(tm)}\end{array}\) Vậy \(S = \left\{ { - 4;4} \right\}\) Đáp án A.
Câu 5 :
Giải phương trình \(f''\left( x \right) = 0\), biết \(f\left( x \right) = {x^3} - 3{x^2}\).
Đáp án : D Phương pháp giải :
Sử dụng công thức \({\left( {{x^n}} \right)'} = n{x^{n - 1}}{\mkern 1mu} {\mkern 1mu} \left( {x \ne {\rm{\;}} - 1} \right)\). Lời giải chi tiết :
\(\begin{array}{*{20}{l}}{f'\left( x \right) = 3{x^2} - 6x \Rightarrow f''\left( x \right) = 6x - 6}\\{ \Rightarrow f''\left( x \right) = 0 \Leftrightarrow 6x - 6 = 0 \Leftrightarrow x = 1}\end{array}\) Đáp án D.
Câu 6 :
Đạo hàm của hàm số \(y = 2{{\rm{x}}^2} - 3{\rm{x}} + 7\) là:
Đáp án : A Phương pháp giải :
Sử dụng công thức đạo hàm của các hàm cơ bản. Lời giải chi tiết :
Ta có: \(y = 2{x^2} - 3x + 7\)\( \Rightarrow y' = 4x - 3\) Đáp án A.
Câu 7 :
Cho A,B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
Đáp án : A Phương pháp giải :
Cho hai biến cố A, B bất kì ta có: \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\) Lời giải chi tiết :
Ta có \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right)\). Vì A,B là hai biến cố xung khắc nên \(A \cap B = \emptyset \). Từ đó suy ra \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\). Đáp án A.
Câu 8 :
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và \(OA = OB = OC = a\). Thể tích của khối tứ diện OABC bằng
Đáp án : D Phương pháp giải :
\({V_{O.ABC}} = \frac{1}{3}OA.{S_{OBC}} = \frac{1}{6}OA.OB.OC\) Lời giải chi tiết :
Từ giả thiết ta thấy \(OA \bot (OBC)\) và OBC là tam giác vuông nên thể tích cần tìm là: \({V_{O.ABC}} = \frac{1}{3}OA.{S_{OBC}} = \frac{1}{6}OA.OB.OC = \frac{{{a^3}}}{6}\) Đáp án D.
Câu 9 :
Tập nghiệm của bất phương trình \(\frac{1}{{{2^x}}} > 8\) là
Đáp án : B Phương pháp giải :
\({a^x} < b \Leftrightarrow x > {\log _a}b\) với \(0 < a < 1\) \({a^x} < b \Leftrightarrow x < {\log _a}b\) với \(a > 1\) Lời giải chi tiết :
\(\frac{1}{{{2^x}}} > 8 \Leftrightarrow {2^{ - x}} > {2^3} \Leftrightarrow {\rm{ \;}} - x > 3 \Leftrightarrow x < {\rm{ \;}} - 3\) Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 3} \right)\) Đáp án B.
Câu 10 :
Cho hình chóp S.ABC có đáy ABC vuông cân tại B,\(AB = BC = a,SA = a\sqrt 3 ,\)\(SA \bot \left( {ABC} \right)\). Số đo của góc phẳng nhị diện \(\left[ {S,BC,A} \right]\) là
Đáp án : D Phương pháp giải :
Xác định góc giữa hai mặt phẳng tạo thành. Lời giải chi tiết :
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AB}\\{BC \bot SA}\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB} \right.\). Khi đó: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SBC} \right) \cap \left( {ABC} \right) = BC}\\{BC \bot AB}\\{BC \bot SB}\end{array} \Rightarrow \left[ {S,BC,A} \right] = \angle } \right.SBA\). Xét vuông tại \(A\), ta có: \({\rm{tan}}\widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 {\rm{ \;}} \Rightarrow \widehat {SBA} = 60^\circ \). Đáp án D.
Câu 11 :
Hàm số \(y = {\cos ^2}3x\) có đạo hàm là
Đáp án : C Phương pháp giải :
Sử dụng quy tắc tính đạo hàm hàm hợp. Lời giải chi tiết :
Ta có: \(y' = 2cos3x.\left( { - \sin 3x} \right).3 = {\rm{ \;}} - 6\sin 3x.cos3x = {\rm{ \;}} - 3\sin 6x\) Đáp án C.
Câu 12 :
Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là \(\frac{1}{5}\) và \(\frac{2}{7}\). Gọi \(A\) là biến cố: "Cả hai cùng ném bóng trúng vào rổ". Khi đó, xác suất của biến cố \(A\) là bao nhiêu?
Đáp án : D Phương pháp giải :
A,B là hai biến cố độc lập nên: \(P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( B \right)\). Lời giải chi tiết :
Gọi \({\rm{A}}\) là biến cố: "Cả hai cùng ném bóng trúng vào rổ. " Gọi \(X\) là biến cố: "người thứ nhất ném trúng rổ" \( \Rightarrow P\left( X \right) = \frac{1}{5}\). Gọi Y là biến cố: "người thứ hai ném trúng rổ" \( \Rightarrow P\left( Y \right) = \frac{2}{7}\). Ta thấy biến cố X,Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có: \(P\left( A \right) = P\left( {X \cdot Y} \right) = P\left( X \right) \cdot P\left( Y \right) = \frac{1}{5} \cdot \frac{2}{7} = \frac{2}{{35}}\). Đáp án D.
Câu 13 :
Cho hình chóp SABCD có đáy là hình chữ nhật với \(AB = a,AD = 2a\). Biết \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt {15} \). Tính góc giữa SC và mặt phẳng \(\left( {ABCD} \right)\).
Đáp án : B Phương pháp giải :
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng. Lời giải chi tiết :
\((SC,\widehat {(ABD})) = (SC;\widehat {(ABCD})) = (\widehat {SC;AC}) = \widehat {SCA}.\) Xét tam giác vuông SAC, ta có: \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{SA}}{{\sqrt {A{B^2} + B{C^2}} }} = \frac{{a\sqrt {15} }}{{\sqrt {{a^2} + {{(2a)}^2}} }} = \sqrt 3 .\) Suy ra \(\widehat {SCA} = {60^\circ }\). Đáp án B.
Câu 14 :
Tìm tọa độ tiếp điểm của các tiếp tuyến \(\Delta \) với đồ thị của hàm số \(y = \frac{{x - 1}}{{x + 1}}\), biết tiếp tuyến đó song song với đường thẳng \(2x - y - 1 = 0\).
Đáp án : A Phương pháp giải :
Lời giải chi tiết :
ĐKXĐ: \(x \ne - 1\) Ta có \(y = \frac{{x - 1}}{{x + 1}} \Rightarrow y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}}\). Vì tiếp tuyến cần tìm song song với đường thẳng \(2x - y - 1 = 0 \Leftrightarrow y = 2x - 1\). Khi đó ta có \(\frac{2}{{{{\left( {x + 1} \right)}^2}}} = 2 \Leftrightarrow {\left( {x + 1} \right)^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = - 2}\end{array}} \right.\). Với \(x = 0 \Rightarrow y = {\rm{ \;}} - 1\) \( \Rightarrow \) Phương trình tiếp tuyến là \(y = 2\left( {x - 0} \right) - 1 = 2x - 1\) (loại) Với \(x = {\rm{ \;}} - 2 \Rightarrow y = 3\) \( \Rightarrow \) Phương trình tiếp tuyến là \(y = 2\left( {x + 2} \right) + 3 = 2x + 7\) (thỏa mãn) \( \Rightarrow \) Tọa độ tiếp điểm là \(\left( { - 2;3} \right)\). Vậy tọa độ tiếp điểm cần tìm là \(\left( { - 2;3} \right)\). Đáp án A.
Câu 15 :
Cho khối lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng \(a\) và đường thẳng A'B hợp với mặt đáy một góc \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ ABC.A'B'C'.
Đáp án : C Phương pháp giải :
Thể tích của khối lăng trụ có diện tích đáy \(B\), chiều cao \(h\) là \(V = h.B\) Lời giải chi tiết :
Ta có: \(AA' \bot \left( {ABC} \right) \Rightarrow \left( {A'B,\left( {ABC} \right)} \right) = \left( {A'B,AB} \right) = \widehat {A'BA}\) Theo giả thiết \(\widehat {A'BA} = 60^\circ \) Lại có: \(\tan 60^\circ = \frac{{AA'}}{{AB}} \Rightarrow AA' = AB\tan 60^\circ = a\sqrt 3 \) Thể tích khối lăng trụ đã cho là \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}}}{4}\) Đáp án C.
Câu 16 :
Cho khối chóp có diện tích đáy bằng \(7{a^2}\) và chiều cao bằng 9a. Thể tích của khối chóp đã cho bằng
II. Trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 3. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Hai xạ A và B cùng bắn vào một mục tiêu. Xác suất trúng mục tiêu của xạ thủ thứ nhất là 0,7 . Xác suất trúng mục tiêu của xạ thủ thứ hai là 0,8 . Gọi A là biến cố: “xạ thủ thứ nhất bắn trúng”, B là biến cố: “xạ thủ thứ hai bắn trúng” Các Khẳng định dưới đây đúng hay sai? a) Khi đó \(A \cup B\) là biến cố: “Cả hai xạ thủ đều bắn trúng”
Đúng
Sai
b) Biến cố \(A \cup B\) và \(A \cap B\) là hai biến cố xung khắc
Đúng
Sai
c) Xác suất để cả hai người bắn trượt là: 0,6
Đúng
Sai
d) Xác suất để có ít nhất một người bắn trúng đích là: 0,94.
Đúng
Sai
Đáp án
a) Khi đó \(A \cup B\) là biến cố: “Cả hai xạ thủ đều bắn trúng”
Đúng
Sai
b) Biến cố \(A \cup B\) và \(A \cap B\) là hai biến cố xung khắc
Đúng
Sai
c) Xác suất để cả hai người bắn trượt là: 0,6
Đúng
Sai
d) Xác suất để có ít nhất một người bắn trúng đích là: 0,94.
Đúng
Sai
Phương pháp giải :
Dùng kiến thức về biến cố, biến cố đối, biến cố xung khắc, xác suất của biến cố Lời giải chi tiết :
a) Sai. Vì \(A \cup B\) là biến cố: “xạ thủ A bắn trúng hoặc xạ thủ B bắn trúng”. b) Sai. Vì biến cố \(A \cap B\) nằm trong \(A \cup B\). c) Sai. Vì xác suất để A và B bắn trượt lần lượt là: 0,3 và 0,4. Xác suất cả hai người bắn trượt là: 0,06 d) Đúng. Vì xác suất để có ít nhất một người bắn trúng đích là biến cố đối của biến cố cả hai người đều bắn trượt: 1 – 0,06 = 0,94
Câu 2 :
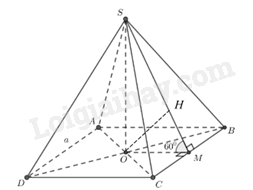
Cho khối chóp đều \(S \cdot ABCD\) có cạnh đáy là \(a\), các mặt bên tạo với đáy một góc \(60^\circ \), O là tâm đáy. Khẳng định sau đây đúng hay sai? a) Thể tích hình chóp là: \(\frac{{{a^3}\sqrt 3 }}{2}\)
Đúng
Sai
b) Độ dài cạnh bên của hình chóp là: \(\frac{{a\sqrt 5 }}{2}\)
Đúng
Sai
c) Khoảng cách \(d\left( {O;\left( {SCB} \right)} \right)\) bằng: \(\frac{{a\sqrt 3 }}{4}\)
Đúng
Sai
d) Khoảng cách \(d\left( {AD;SC} \right) = \frac{{a\sqrt 3 }}{3}\)
Đúng
Sai
Đáp án
a) Thể tích hình chóp là: \(\frac{{{a^3}\sqrt 3 }}{2}\)
Đúng
Sai
b) Độ dài cạnh bên của hình chóp là: \(\frac{{a\sqrt 5 }}{2}\)
Đúng
Sai
c) Khoảng cách \(d\left( {O;\left( {SCB} \right)} \right)\) bằng: \(\frac{{a\sqrt 3 }}{4}\)
Đúng
Sai
d) Khoảng cách \(d\left( {AD;SC} \right) = \frac{{a\sqrt 3 }}{3}\)
Đúng
Sai
Phương pháp giải :
a) Thể tích của khối chóp có diện tích đáy \(B\), chiều cao \(h\) là \(V = \frac{1}{3}h.B\) b) Áp dụng định lí Pytago c) Áp dụng hệ thức lượng trong tam giác vuông d) \(d\left( {AD;SC} \right) = 2d\left( {O;\left( {SCB} \right)} \right)\) Lời giải chi tiết :
a) Sai. Gọi \(M\) là trung điểm BC, Góc giữa mặt bên \((SBC)\) và mặt phẳng \((ABCD)\) là góc \(\widehat {SMO} = 60^\circ \). Xét \(\Delta SOM\) có \(OM = \frac{a}{2},SMO = 60^\circ \) thì \(SO = OM \cdot \tan \widehat {SMO} = \frac{a}{2} \cdot \sqrt 3 = \frac{{a\sqrt 3 }}{2}\) Nên \({V_{S.ABCD}} = \frac{1}{3}SO{S_{AGCD}} = \frac{{{a^3}\sqrt 3 }}{6}(dvtt)\). b) Đúng. Đúng. Xét \(\Delta SOB\) vuông tại O ta có: \(SB = \sqrt {O{M^2} + O{B^2}} = \sqrt {\frac{{3{a^2}}}{4} + \frac{{2{a^2}}}{4}} = \frac{{\sqrt 5 a}}{2}\). c) Đúng. Kẻ OH vuông góc với SM khi đó \(d\left( {O;\left( {SCB} \right)} \right) = OH\) Xét \(\Delta SOM\)vuông tại O có: \(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} = \frac{{16}}{{3{a^2}}} \Rightarrow OH = \frac{{a\sqrt 3 }}{4}\) d) Sai Vì \(AD//CB\) mà \(CB \subset \left( {SBC} \right)\) nên \(d\left( {AD;SC} \right) = d\left( {AD;\left( {SCB} \right)} \right) = d\left( {A;\left( {SCB} \right)} \right) = 2d\left( {O;\left( {SCB} \right)} \right) = \frac{{a\sqrt 3 }}{2}\)
Câu 3 :
Cho hàm số \(f(x) = - \frac{m}{3}{x^3} + m{x^2} - 3x + 9\), \(g\left( x \right) = 2{x^3} - 6x + 1\) a) Phương trình tiếp tuyến của hàm \(g\left( x \right)\) tại \(x = 3\) là: \(y = 3x + 107\)
Đúng
Sai
b) Phương trình tiếp tuyến của \(g\left( x \right)\) song song với đường thẳng \(y = - 6x - 5\) là: \(y = - 6x + 1\)
Đúng
Sai
c) Phương trình \(f'\left( x \right) = g'\left( x \right)\) có hai nghiệm phân biệt với mọi \(m \in \mathbb{R}\)
Đúng
Sai
d) Để \(f'(x) \le 0\forall x \in \mathbb{R}\) thì \(m\).
Đúng
Sai
Đáp án
a) Phương trình tiếp tuyến của hàm \(g\left( x \right)\) tại \(x = 3\) là: \(y = 3x + 107\)
Đúng
Sai
b) Phương trình tiếp tuyến của \(g\left( x \right)\) song song với đường thẳng \(y = - 6x - 5\) là: \(y = - 6x + 1\)
Đúng
Sai
c) Phương trình \(f'\left( x \right) = g'\left( x \right)\) có hai nghiệm phân biệt với mọi \(m \in \mathbb{R}\)
Đúng
Sai
d) Để \(f'(x) \le 0\forall x \in \mathbb{R}\) thì \(m\).
Đúng
Sai
Phương pháp giải :
a) Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\). b) Hai đường thẳng song song khi chúng có hệ số góc bằng nhau c) Phương trình bậc hai có 2 nghiệm phân biệt khi \(\Delta > 0\) hoặc \(\Delta ' > 0\) d) Chia trường hợp rồi tìm các giá trị m thỏa mãn Lời giải chi tiết :
a) Sai Ta có: \(g'\left( x \right) = 6{x^2} - 6 \Rightarrow g'\left( 3 \right) = 48\) Ta có \(x = 3 \Rightarrow g\left( 3 \right) = 37 \Rightarrow A\left( {3;37} \right)\) Phương trình tiếp tuyến qua điểm \(A\left( {3;37} \right)\) là: \(y = 48\left( {x - 3} \right) + 37 \Rightarrow y = 3x - 107\) b) Đúng. Phương trình tiếp tuyến của \(g\left( x \right)\) song song với đường thẳng \(y = - 6x - 5\) nên ta có hệ số góc bẳng \( - 6\) \( \Rightarrow g'\left( x \right) = 6{x^2} - 6 = - 6 \Leftrightarrow x = 0 \Rightarrow g\left( 0 \right) = 1\) vậy \(B\left( {0;1} \right)\) Phương trình tiếp tuyến qua điểm \(B\left( {0;1} \right)\) là: \(y = - 6\left( {x - 0} \right) + 1 = - 6x + 1\) c) Sai Ta có \(f'\left( x \right) = g'\left( x \right)\) \(\begin{array}{l} \Leftrightarrow - m{x^2} + 2mx - 3 = 6{x^2} - 6\\ \Leftrightarrow \left( {m + 6} \right){x^2} - 2mx - 3 = 0\end{array}\) Để phương trình có hai nghiệm phân biệt thì \(\left\{ \begin{array}{l}m + 6 \ne 0\\\Delta ' = {m^2} + 3\left( {m + 6} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne - 6\\\Delta ' = {m^2} + 3\left( {m + 6} \right) > 0,\forall m \in \mathbb{R}\end{array} \right.\) Vậy để phương trình có hai nghiệm phân biệt thì \(m \ne - 6\). d) Tìm tất cả các giá trị của \(m\) để \(f'(x) \le 0\forall x \in \mathbb{R}\). \(f(x) = - \frac{m}{3}{x^3} + m{x^2} - 3x + 9\) \( \Rightarrow f'(x) = - m{x^2} + 2mx - 3\) \(f'(x) \le 0\forall x \in \mathbb{R} \Leftrightarrow - m{x^2} + 2mx - 3 \le 0\forall x \in \mathbb{R}\) \({\rm{TH1: }}m = 0 \Rightarrow f'(x) = - 3 \le 0\forall x \in \mathbb{R}{\rm{ }}\) \({\rm{TH2: }}m \ne 0\) \( - m{x^2} + 2mx - 3 \le 0\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - m < 0}\\{\Delta ' = {m^2} - 3m \le 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > 0}\\{0 \le m \le 3}\end{array} \Leftrightarrow 0 < m \le 3} \right.} \right.\) Vậy \(0 \le m \le 3\).
III. Tự luận trả lời ngắn
Phương pháp giải :
Ta có: \(s(t)'' = v(t)' = a(t)\) Lời giải chi tiết :
\(s = {t^3} - 3{t^2} - 9t \Rightarrow v(t) = 3{t^2} - 6t - 9 \Rightarrow a(t) = 6t - 6\) \(v = 0 \Rightarrow 3{t^2} - 6t - 9 = 0 \Leftrightarrow t = 3\). Vậy \(a(3) = 6.3 - 6 = 12\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\). Phương pháp giải :
\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\) Lời giải chi tiết :
A, B là hai biến cố bất kỳ ta luôn có: \(P(A \cup B) = P(A) + P(B) - P(A \cap B) = \frac{1}{2} + \frac{3}{4} - \frac{1}{4} = 1\) Phương pháp giải :
Dùng biến cố đối Lời giải chi tiết :
\({n_\Omega } = C_{10}^3 = 120\) Gọi \({\rm{A}}\) là biến cố: "Chọn được 3 số tự nhiên có tích là 1 số chẵn" \(\bar A\) : "Chọn được 3 số tự nhiên có tích là 1 số lẻ". Để chọn được 3 số tự nhiên có tích là 1 số lẻ thì cả 3 số phải cùng lẻ \( \Rightarrow {n_{\bar A}} = C_6^3 = 20 \Rightarrow {n_A} = 120 - 20 = 100.\) Vậy \(P(A) = \frac{{100}}{{120}} = \frac{5}{6}\). Phương pháp giải :
Thể tích của khối lăng trụ có diện tích đáy \(B\), chiều cao \(h\) là \(V = h.B\) Lời giải chi tiết :
Ta có: \(AA' \bot (ABC) \Rightarrow \left( {A'B,(ABC)} \right) = \left( {A'B,AB} \right) = \widehat {A'BA}\) Theo giả thiết \(\widehat {A'BA} = 60^\circ \) Lại có: \(\tan 60^\circ = \frac{{AA'}}{{AB}} \Rightarrow AA' = AB\tan 60^\circ = a\sqrt 3 \) Thể tích khối lăng trụ đã cho là \({V_{ABC \cdot A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}}}{4}\) Phương pháp giải :
\({a^x} = {a^y} \Leftrightarrow x = y\) Lời giải chi tiết :
Ta có: \({27^{2x - 3}} = {\left( {\frac{1}{3}} \right)^{{x^2} + 2}} \Leftrightarrow {3^{6x - 9}} = {3^{ - {x^2} - 2}}\) \( \Leftrightarrow 6x - 9 = - {x^2} - 2 \Leftrightarrow {x^2} + 6x - 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 7}\end{array}} \right.{\rm{ }}\) Vậy tập nghiệm của phương trình là \(\{ 1; - 7\} \) Phương pháp giải :
Sử dụng công thức logarit để giải phương trình Lời giải chi tiết :
\(\log _a^2\left( {{a^2}b} \right) \cdot {\log _a}\frac{b}{a} + 4 = 0{\rm{ }}\) \( \Leftrightarrow {\left( {{{\log }_a}{a^2} + {{\log }_a}b} \right)^2} \cdot \left( {{{\log }_a}b - {{\log }_a}a} \right) = - 4\) \( \Leftrightarrow {\left( {2 + {{\log }_a}b} \right)^2} \cdot \left( {{{\log }_a}b - 1} \right) = - 4\) \( \Leftrightarrow \left( {\log _a^2b + 4{{\log }_a}b + 4} \right)\left( {{{\log }_a}b - 1} \right) = - 4\) \( \Leftrightarrow \log _a^3b + 4\log _a^2b + 4{\log _a}b - \log _a^2b - 4{\log _a}b - 4 = - 4\) \( \Leftrightarrow \log _a^3b + 3\log _a^2b = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\log }_a}b = 0}\\{{{\log }_a}b = - 3}\end{array}} \right.\) Vậy \(S = \left\{ {0; - 3} \right\}\).
|






















Danh sách bình luận