Bài 27 trang 120 Sách bài tập Hình học lớp 12 Nâng cao

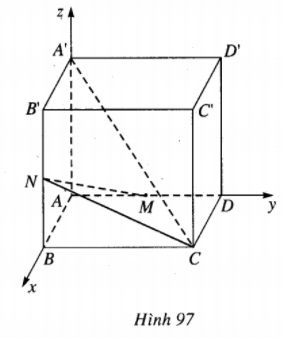
LG a

Chứng minh \({A'C}  \bot (AB'D').\)

Lời giải chi tiết:

Thiết lập hệ trục tọa độ như hình vẽ (h.97).Ta có

A(0;0;0); A’(0;0;a); C’(a;a;a); D(0;a;0)

B(a;0;0); D’(0;a;a); B’(a;0;a), C(a;a;0).

Ta có :

\(\eqalign{  & \overrightarrow {A'C}  = (a;a; - a),  \cr  & \overrightarrow {AB'}  = (a;0;a),\overrightarrow {AD'}  = (0;a;a)  \cr  &  \Rightarrow \overrightarrow {A'C} .\overrightarrow {AB'}  = 0,\overrightarrow {A'C} .\overrightarrow {AD'}  = 0  \cr  &  \Rightarrow \overrightarrow {A'C}  \bot \overrightarrow {{\rm{AB'}}} ,\overrightarrow {A'C}  \bot \overrightarrow {AD'}   \cr  &  \Rightarrow A'C \bot mp(AB'D'). \cr} \)

LG b

Gọi M là trung điểm của AD, N là trung điểm của BB’. Chứng minh \(A'C \bot MN.\)

Lời giải chi tiết:

Ta lại có :

\(\eqalign{  & N(a;0;{a \over 2}),M\left( {0;{a \over 2};0} \right) \Rightarrow \overrightarrow {MN}  = \left( {a; - {a \over 2};{a \over 2}} \right)  \cr  &  \Rightarrow \overrightarrow {MN} .\overrightarrow {A'C}  = {a^2} - {{{a^2}} \over 2} - {{{a^2}} \over 2} = 0 \Rightarrow MN \bot A'C. \cr} \)

LG c

Tính cô sin của góc giữa hai vec tơ \(\overrightarrow {MN} \) và \(\overrightarrow {AC'} \).

Lời giải chi tiết:

\(\overrightarrow {AC'}  = (a;a;a)\) nên

\(\cos \left( {\overrightarrow {MN} ,\overrightarrow {AC'} } \right) = {{\overrightarrow {MN} .\overrightarrow {AC'} } \over {\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {AC'} } \right|}} = {{{a^2} - {{{a^2}} \over 2} + {{{a^2}} \over 2}} \over {\sqrt {{{3{a^2}} \over 2}} .\sqrt {3{a^2}} }} = {{\sqrt 2 } \over 3}\)

LG d

Tính \({V_{A'CMN}}\)

Lời giải chi tiết:

\(\eqalign{  & {V_{A'CMN}} = {1 \over 6}\left| {\left[ {\overrightarrow {A'N} .\overrightarrow {A'M} } \right].\overrightarrow {A'C} } \right|.  \cr  &  \cr} \)

Ta có :

\(\eqalign{  & \overrightarrow {A'N}  = (a;0; - {a \over 2}),\overrightarrow {A'M}  = \left( {0;{a \over 2}; - a} \right).  \cr  &   \left[ {\overrightarrow {A'N} ,\overrightarrow {A'M} } \right] = \left( {\left| \matrix{  0 \hfill \cr  {a \over 2} \hfill \cr}  \right.\left. \matrix{   - {a \over 2} \hfill \cr   - a \hfill \cr}  \right|;\left| \matrix{   - {a \over 2} \hfill \cr  a \hfill \cr}  \right.\left. \matrix{  a \hfill \cr   \hfill \cr  0 \hfill \cr}  \right|;\left| \matrix{  a \hfill \cr   \hfill \cr  0 \hfill \cr}  \right.\left. \matrix{  0 \hfill \cr  {a \over 2} \hfill \cr}  \right|} \right) \cr&= \left( {{{{a^2}} \over 4};{a^2};{{{a^2}} \over 2}} \right)  \cr  &  \Rightarrow {V_{A'CMN}} = {1 \over 6}\left| {{{{a^3}} \over 4} + {a^3} - {{{a^3}} \over 2}} \right| = {1 \over 6}\left| {{{3{a^3}} \over 4}} \right| = {{{a^3}} \over 8}. \cr} \)

Loigiaihay.com