Bài 31 trang 121 Sách bài tập Hình học lớp 12 Nâng caoa)Viết phương trình mặt cầu đi qua Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
LG a Viết phương trình mặt cầu đi qua A(1;2;-4), B(1;-3;1), C(2;2;3) và có tâm nằm trên mp(Oxy). Lời giải chi tiết: Gọi I là tâm mặt cầu. Vì \(I \in mp(Oxy)\) nên I=(x;y;0). Theo giả thiết, ta có \(A{I^2} = B{I^2} = C{I^2}\), suy ra
\(\Rightarrow \left\{ \matrix{ x = - 2 \hfill \cr y = 1 \hfill \cr} \right. \Rightarrow I( - 2;1;0). \) Bán kính của mặt cầu là: \(R = AI = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {1 - 2} \right)}^2} + {4^2}} = \sqrt {26} \) Vậy phương trình mặt cầu là: \({(x + 2)^2} + {(y - 1)^2} + {z^2} = 26.\) LG b Viết phương trình mặt cầu đi qua hai điểm A(3;-1;2), B(1;1;-2) và có tâm thuộc trục Oz. Lời giải chi tiết: Gọi I là tâm mặt cầu, \(I \in Oz\) nên I = (0;0;z). Theo giả thiết \(A{I^2} = B{I^2}\), ta có phương trình \({( - 3)^2} + {1^2} + {(z - 2)^2} = {( - 1)^2} + {( - 1)^2} + {(z + 2)^2}\) \(\Rightarrow 8z = 8 \Rightarrow z = 1\) Vậy \(I=(0;0;1)\) và \(AI = \sqrt {11} .\) Phương trình mặt cầu cần tìm là \({x^2} + {y^2} + {(z - 1)^2} = 11\) LG c Viết phương trình mặt cầu đi qua bốn điểm A(1;1;1), B(1;2;1), C(1;1;2), D(2;2;1). Lời giải chi tiết: Phương trình mặt cầu (S) cần tìm có dạng Ta có : \(\eqalign{ & {(x)^2} + {(y)^2} + {(z)^2} - 2ax - 2by - 2cz + d = 0 \cr & A \in (S) \Leftrightarrow 2a + 2b + 2c - d = 3. \cr & B \in (S) \Leftrightarrow 2a + 4b + 2c - d = 6. \cr & C \in (S) \Leftrightarrow 2a + 2b + 4c - d = 6. \cr & D \in (S) \Leftrightarrow 4a + 4b + 2c - d = 9. \cr} \) Từ đó ta suy ra \(a = {3 \over 2};b = {3 \over 2};c = {3 \over 2};d = 6.\) Vậy phương trình mặt cầu là : \({x^2} + {y^2} + {z^2} - 3x - 3y - 3z + 6 = 0.\) Loigiaihay.com
|














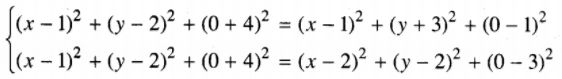






Danh sách bình luận