Bài 28 trang 120 Sách bài tập Hình học lớp 12 Nâng cao

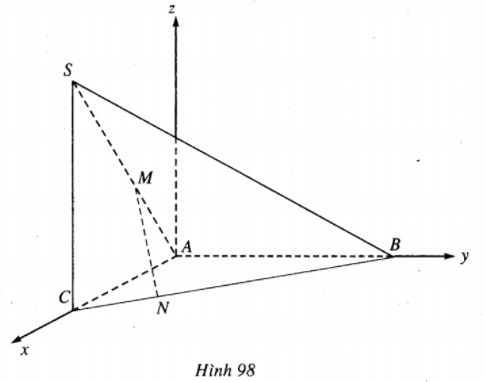
LG a

Tính độ dài đoạn MN. Tìm giá trị t để MN ngắn nhất.

Lời giải chi tiết:

Ta chọn hệ trục Oxyz sao cho gốc tọa độ O trùng A, tia Ox chứa AC, tia Oy chứa AB và tia Oz cùng hướng tới tia CS (h.98). Khi đó, ta có:

\(A(0;0;0),B(0;a\sqrt 2 ;0),C(a\sqrt 2 ;0;0),\)

\(S(a\sqrt 2 ;0;a\sqrt 2 ),\)

\(\eqalign{  & M\left( {{{t\sqrt 2 } \over 2};0;{{t\sqrt 2 } \over 2}} \right);N\left( {a\sqrt 2  - {{t\sqrt 2 } \over 2};{{t\sqrt 2 } \over 2};0} \right)  \cr  &  \Rightarrow \overrightarrow {MN}  = \left( {\sqrt 2 (a - t);{{t\sqrt 2 } \over 2}; - {{t\sqrt 2 } \over 2}} \right)  \cr  &  \Rightarrow  {MN}  = \sqrt {2({a^2} - 2at + {t^2}) + {{{t^2}} \over 2} + {{{t^2}} \over 2}}  \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {3{t^2} - 4at + 2{a^2}}   \cr  &  \;\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {3{{\left( {t - {{2a} \over 3}} \right)}^2} + {{2{a^2}} \over 3}}  \ge {{a\sqrt 6 } \over 3}. \cr} \)

Dấu "=" xảy ra khi \(t = {{2a} \over 3}\) thỏa mãn điều kiện 0 < t < 2a.

Vậy MN ngắn nhất bằng \({{a\sqrt 6 } \over 3}\) khi \(t = {{2a} \over 3}.\)

LG b

Khi đoạn MN ngắn nhất, chứng minh MN là đường vuông góc chung của BC và SA.

Lời giải chi tiết:

Khi MN ngắn nhất thì :

\(\overrightarrow {MN}  = \left( {{{a\sqrt 2 } \over 3};{{a\sqrt 2 } \over 3}; - {{a\sqrt 2 } \over 3}} \right) \Rightarrow \left\{ \matrix{  \overrightarrow {MN} .\overrightarrow {SA}  = 0 \hfill \cr  \overrightarrow {MN} .\overrightarrow {BC}  = 0 \hfill \cr}  \right.\)

\( \Rightarrow MN\) là đường vuông góc chung của SA và BC.

Loigiaihay.com