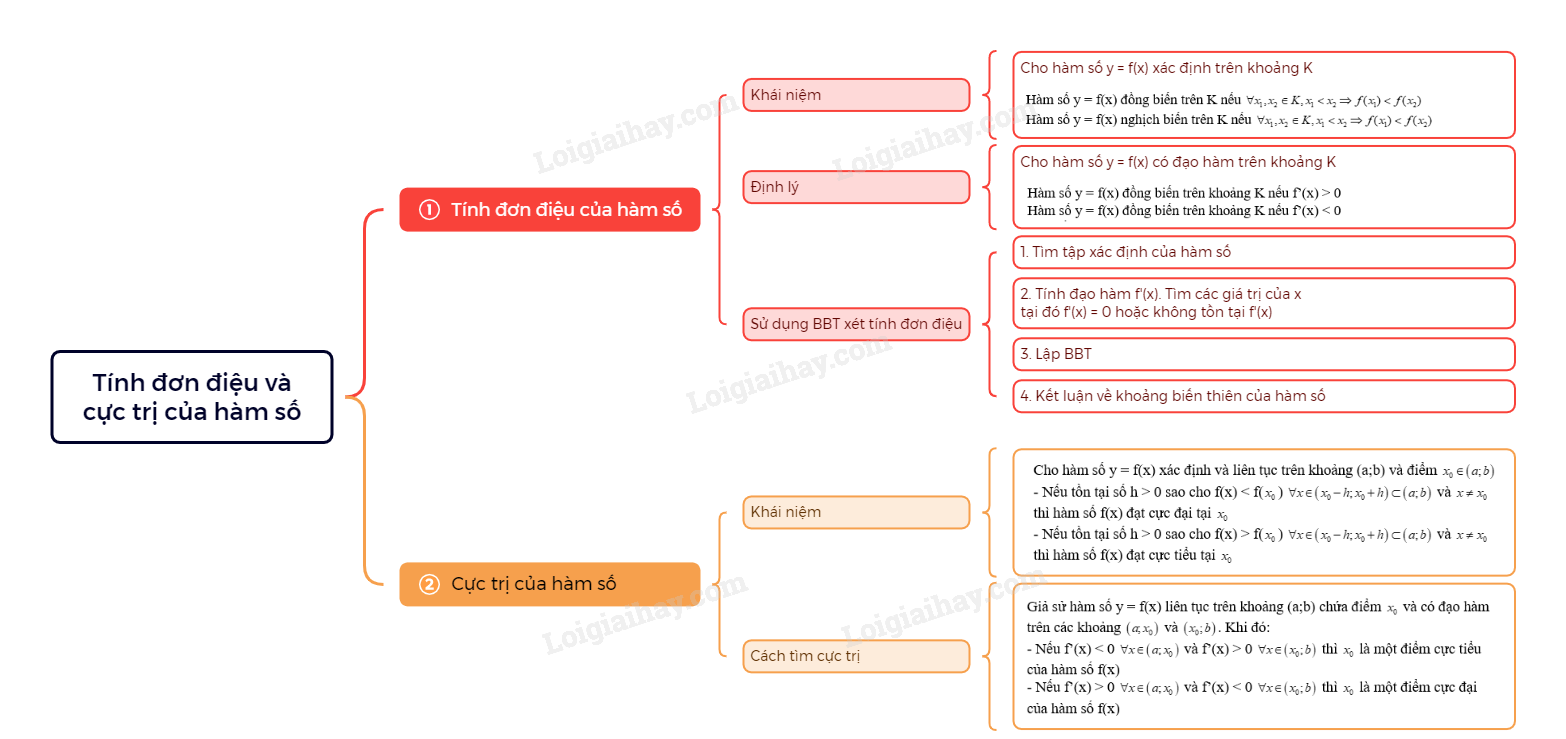
1. Tính đơn điệu của hàm số
Khái niệm tính đơn điệu của hàm số
|
Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là hàm số xác định trên K.
- Hàm số y = f(x) đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\).
- Hàm số y = f(x) nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\).
|
Ví dụ: Hàm số y = |x| đồng biến trên khoảng \(\left( {0; + \infty } \right)\), nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Định lý
|
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
- Hàm số y = f(x) đồng biến trên khoảng K nếu f’(x) > 0.
- Hàm số y = f(x) đồng biến trên khoảng K nếu f’(x) < 0.
|
Ví dụ: Hàm số \(y = {x^2} - 4x + 2\) có y’ = 2x – 4
- y’ > 0 với \(x \in (2; + \infty )\) nên HS đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
- y’ < 0 với \(x \in ( - \infty ;2)\) nên HS đồng biến trên khoảng \(\left( { - \infty ;2} \right)\).
Sử dụng BBT xét tính đơn điệu của hàm số
|
Các bước để xét tính đơn điệu của hàm số y = f(x)
- Tìm tập xác định của hàm số.
- Tính đạo hàm f’(x). Tìm các điểm \({x_i}\) (i = 1, 2,…) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
- Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập BBT của hàm số.
- Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
|
Ví dụ: Xét chiều biến thiên của hàm số \(y = \frac{{x - 2}}{{x + 1}}\).
1. Tập xác định của hàm số là \(R\backslash \left\{ { - 1} \right\}\).
2. Ta có: \(y' = \frac{{(x + 1) - (x - 2)}}{{{{(x + 1)}^2}}} = \frac{3}{{{{(x + 1)}^2}}} > 0\forall x \ne - 1\).
3. Bảng biến thiên:
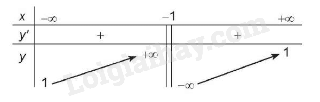
4. Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
2. Cực trị của hàm số
Khái niệm cực trị của hàm số
|
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b) (a có thể là \( - \infty \), b có thể là \( + \infty \) ) và điểm \({x_0} \in \left( {a;b} \right)\).
- Nếu tồn tại số h > 0 sao cho f(x) < f(\({x_0}\)) \(\forall x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì hàm số f(x) đạt cực đại tại \({x_0}\).
- Nếu tồn tại số h > 0 sao cho f(x) > f(\({x_0}\)) \(\forall x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì hàm số f(x) đạt cực tiểu tại \({x_0}\).
|
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau:
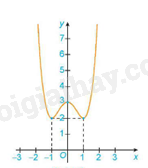
Hàm số đạt cực tiểu tại x = -1 và \({y_{CT}}\) = y(-1) = 2.
Hàm số đạt cực đại tại x = 0 và = y(0) = 3.
Hàm số đạt cực tiểu tại x = 1 và \({y_{CT}}\)= y(1) = 2.
Cách tìm cực trị của hàm số
|
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
- Nếu f’(x) < 0 \(\forall x \in \left( {a;{x_0}} \right)\) và f’(x) > 0 \(\forall x \in \left( {{x_0};b} \right)\) thì \({x_0}\) là một điểm cực tiểu của hàm số f(x)
- Nếu f’(x) > 0 \(\forall x \in \left( {a;{x_0}} \right)\) và f’(x) < 0 \(\forall x \in \left( {{x_0};b} \right)\) thì \({x_0}\) là một điểm cực đại của hàm số f(x)
|
Ví dụ: Tìm cực trị của hàm số \(y = {x^3} - 6{x^2} + 9x + 30\).
Tập xác định của hàm số là R.
Ta có: \(y' = 3{x^2} - 12x + 9\); y’ = 0 \( \Leftrightarrow \) x = 1 hoặc x = 3.
Bảng biến thiên:

Hàm số đạt cực đại tại x = 1 và = y(1) = 34.
Hàm số đạt cực tiểu tại x = 3 và \({y_{CT}}\)= y(3) = 30.
























Danh sách bình luận