Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Kết nối tri thức1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto Quảng cáo
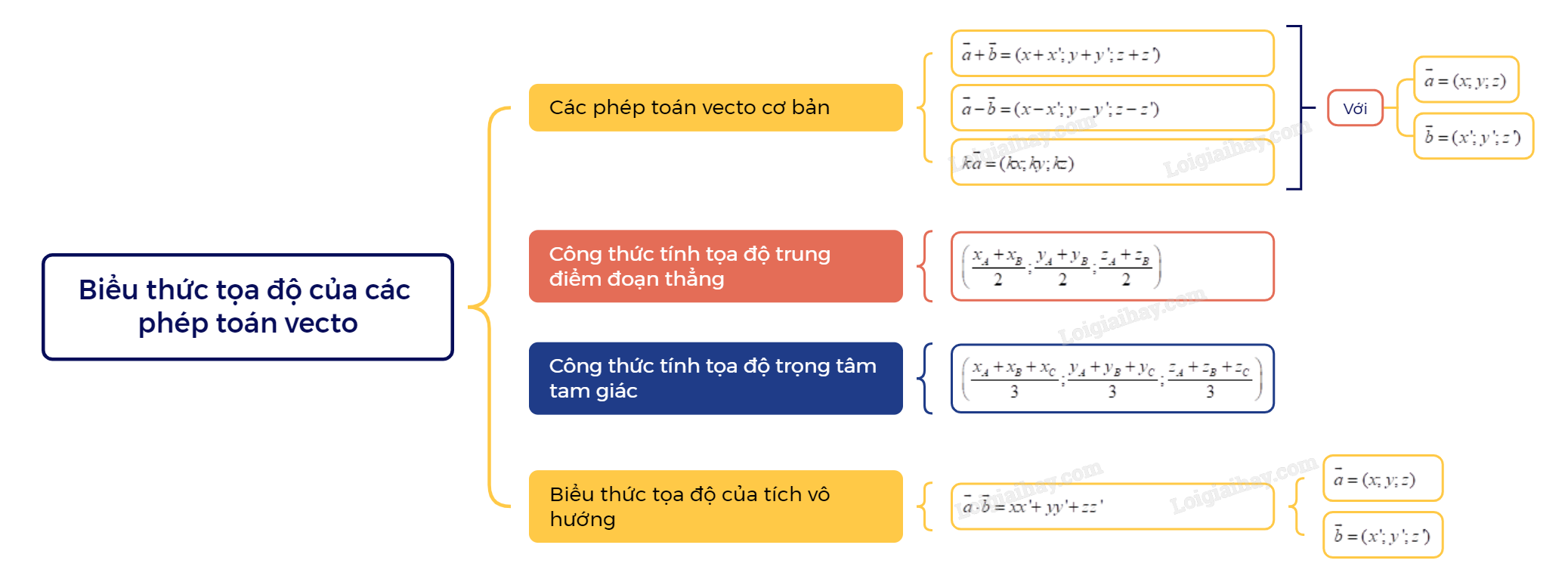
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto Các phép toán vecto cơ bản
Công thức tính tọa độ trung điểm đoạn thẳng và trọng tâm tam giác
2. Biểu thức tọa độ của tích vô hướng
3. Vận dụng tọa độ của vecto trong một số bài toán có liên quan đến thực tiễn Ví dụ: Trong không gian với một hệ trục cho trước (đơn vị đo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B (940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 5 phút tiếp theo là gì? Giải: Gọi C(x;y;z) là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng. Do vận tốc bay không đổi và thời gian bay từ A đến B gấp đôi thời gian bay từ B đến C nên AB = 2BC. Do đó, \(\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AB} = \left( {\frac{{940 - 800}}{2};\frac{{550 - 500}}{2};\frac{{8 - 7}}{2}} \right) = \left( {70;25;0,5} \right)\). Mặt khác, \(\overrightarrow {BC} = (x - 940;y - 550;z - 8)\) nên \(\left\{ \begin{array}{l}x - 940 = 70\\y - 550 = 25\\z - 8 = 0,5\end{array} \right.\). Từ đó \(\left\{ \begin{array}{l}x = 1010\\y = 575\\z = 8,5\end{array} \right.\) và vì vậy C(1010;575;8,5). Vậy tọa độ của máy bay sau 5 phút tiếp theo là (1010;575;8,5).
|




















Danh sách bình luận