Phần câu hỏi bài 7 trang 47, 48 Vở bài tập toán 7 tập 2Giải phần câu hỏi bài 7 trang 47, 48 VBT toán 7 tập 2. Khoanh tròn vào số là bậc của đa thức... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Câu 19 Khoanh tròn vào số là bậc của đa thức.
Phương pháp giải: - Thu gọn đa thức nếu có. - Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó. Lời giải chi tiết: Đa thức \({x^2} + 2x - 3{x^3} + 2{x^5} + 3{x^4} - 1\) có bậc \(5\). \({x^6} + 2{x^5} - 3{x^6} + 2{x^5} + 2{x^6} - {x^3} + {x^2} \)\(\,+ 1\) \(= \left( {{x^6} - 3{x^6} + 2{x^6}} \right) + \left( {2{x^5} + 2{x^5}} \right)\)\(\, - {x^3} + {x^2} + 1\) \(= 4{x^5} - {x^3} + {x^2} + 1\) Do đó đa thức \({x^6} + 2{x^5} - 3{x^6} + 2{x^5} + 2{x^6} - {x^3} + {x^2} \)\(\,+ 1\) có bậc \(5\). \({\left( {x - 2} \right)^2} + 2x - 3{x^2} + 3\) \(= \left( {x - 2} \right)\left( {x - 2} \right) + 2x - 3{x^2} + 3\) \(= x.x + x.\left( { - 2} \right) + \left( { - 2} \right).x \)\(\,+ \left( { - 2} \right).\left( { - 2} \right)\)\(\, + 2x - 3{x^2} + 3\) \(= {x^2} - 2x - 2x + 4 + 2x - 3{x^2} + 3\) \(= \left( {{x^2} - 3{x^2}} \right) + \left( { - 2x - 2x + 2x} \right) \)\(\,+ \left( {4 + 3} \right)\) \(= - 2{x^2} - 2x + 7\) Do đó đa thức \({\left( {x - 2} \right)^2} + 2x - 3{x^2} + 3\) có bậc \(2\). \(\begin{array}{l} Do đó đa thức \(2{x^5} + 3{x^4} - {x^8} + {x^5} + 1\) có bậc \(8\). Ta khoanh như sau:
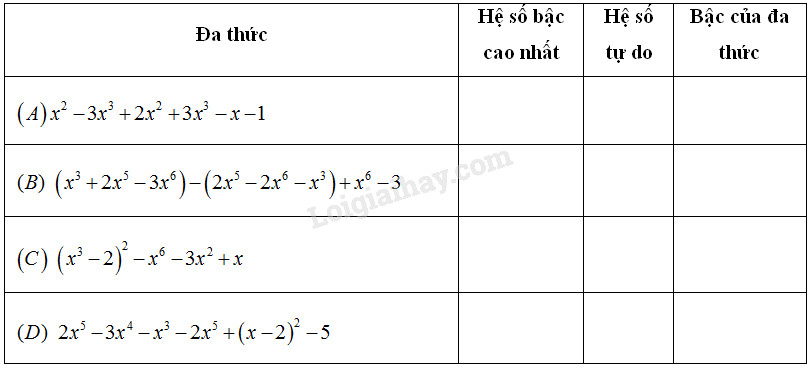
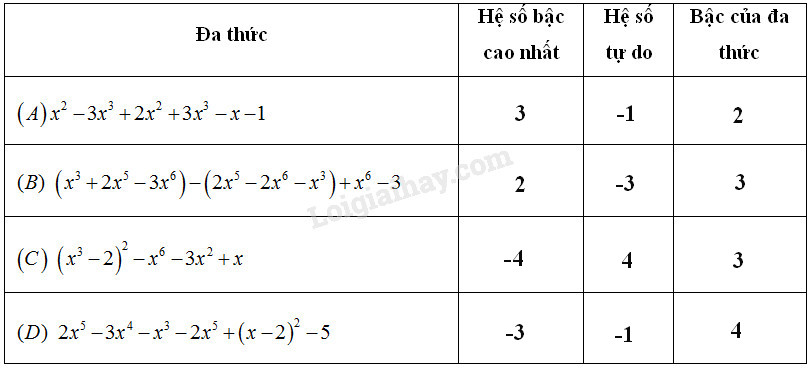
Câu 20 Điền vào ô trống trong bảng sau :
Phương pháp giải: Ta thu gọn đa thức đã cho sau đó trong dạng thu gọn của đa thức: - Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất. - Hệ số của hạng tử bậc không gọi là hệ số tự do. Lời giải chi tiết: \({x^2} - 3{x^3} + 2{x^2} + 3{x^3} - x - 1\) \(= \left( { - 3{x^3} + 3{x^3}} \right) + \left( {{x^2} + 2{x^2}} \right) - x \)\(\,- 1\) \(= 3{x^2} - x - 1\) Hệ số bậc cao nhất là:\(3\) Hệ số tự do là: \(-1\) Bậc của đa thức là: \(2\) \(\left( {{x^3} + 2{x^5} - 3{x^6}} \right) - \left( {2{x^5} - 2{x^6} - {x^3}} \right) \)\(\,+ {x^6} - 3\) \(= {x^3} + 2{x^5} - 3{x^6} - 2{x^5} + 2{x^6} + {x^3}\)\(\, + {x^6} - 3\) \(= \left( { - 3{x^6} + 2{x^6} + {x^6}} \right) + \left( {2{x^5} - 2{x^5}} \right) \)\(\,+ \left( {{x^3} + {x^3}} \right) - 3\) \(= 2{x^3} - 3\) Hệ số bậc cao nhất là: \(2\) Hệ số tự do là: \(-3\) Bậc của đa thức là: \(3\) \({\left( {{x^3} - 2} \right)^2} - {x^6} - 3{x^2} + x\) \(= \left( {{x^3} - 2} \right).\left( {{x^3} - 2} \right) - {x^6} - 3{x^2} + x\) \(= {x^3}.{x^3} + {x^3}.\left( { - 2} \right) + \left( { - 2} \right).{x^3} \)\(\,+ \left( { - 2} \right).\left( { - 2} \right) - {x^6} - 3{x^2} + x\) \(= {x^6} - 2{x^3} - 2{x^3} + 4 - {x^6} - 3{x^2} + x\) \(= \left( {{x^6} - {x^6}} \right) + \left( { - 2{x^3} - 2{x^3}} \right) - 3{x^2} \)\(\,+ x + 4\) \(= - 4{x^3} - 3{x^2} + x + 4\) Hệ số bậc cao nhất là: \(-4\) Hệ số tự do là: \(4\) Bậc của đa thức là: \(3\) \(2{x^5} - 3{x^4} - {x^3} - 2{x^5} + {\left( {x - 2} \right)^2} - 5\) \(= 2{x^5} - 3{x^4} - {x^3} - 2{x^5} \)\(\,+ \left( {x - 2} \right).\left( {x - 2} \right) - 5\) \(= 2{x^5} - 3{x^4} - {x^3} - 2{x^5} + x.x \)\(\,+ x.\left( { - 2} \right) + \left( { - 2} \right).x + \left( { - 2} \right).\left( { - 2} \right)\)\(\, - 5\) \(= 2{x^5} - 3{x^4} - {x^3} - 2{x^5} + {x^2} \)\(\,- 2x - 2x + 4 - 5\) \(= \left( {2{x^5} - 2{x^5}} \right) - 3{x^4} - {x^3} + {x^2} \)\(\,+ \left( { - 2x - 2x} \right) - 1\) \(= - 3{x^4} - {x^3} + {x^2} - 4x - 1\) Hệ số bậc cao nhất là: \(-3\) Hệ số tự do là: \(-1\) Bậc của đa thức là: \(4\) Ta điền vào bảng như sau:
Câu 21 Điền “\( \times \)” vào ô trống trong bảng sau :
Phương pháp giải: - Thay giá trị của biến vào đa thức. - Tính rồi tích vào ô trống thích hợp. Lời giải chi tiết: (A) Thay \(x = - 1\) vào đa thức \({x^5} + \dfrac{1}{3}{x^2} - \dfrac{5}{6}{x^4} + 2{x^3} - 6x - 12\) ta được: \( {\left( { - 1} \right)^5} + \dfrac{1}{3} \cdot {\left( { - 1} \right)^2} - \dfrac{5}{6} \cdot {\left( { - 1} \right)^4}\)\( + 2.{\left( { - 1} \right)^3} - 6.\left( { - 1} \right) - 12\) \( = - 1 + \dfrac{1}{3} - \dfrac{5}{6} - 2 + 6 - 12\) \( = \) \( - \dfrac{{19}}{2}\) (B) Với \(x = - 2\) thì \(5{x^6} - {x^5} - 3x + 4{x^4} - 4{x^3} - 2\) \( = 5.{\left( { - 2} \right)^6} - {\left( { - 2} \right)^5} - 3.\left( { - 2} \right) \)\(\,+ 4.{\left( { - 2} \right)^4}\)\(- 4.{\left( { - 2} \right)^3} - 2\) \( = 452\) (C) Với \(x = - 1\)thì \(\left| {{x^4} - 5{x^3}} \right| + \left| {{x^5} - 5{x^3}} \right| - \left( {3{x^2} - {x^4}} \right)\)\( + 2008\) \( = \left| {{{\left( { - 1} \right)}^4} - 5.{{\left( { - 1} \right)}^3}} \right|\)\(\,+ \left| {{{\left( { - 1} \right)}^5} - 5.{{\left( { - 1} \right)}^3}} \right|\)\( - \left[ {3.{{\left( { - 1} \right)}^2} - {{\left( { - 1} \right)}^4}} \right] + 2008\) \( = \left| 6 \right| + \left| 4 \right| - 2 + 2008\) \( = 2016\) Vậy (A) – Sai; (B) – Sai; (C) – Đúng. Loigiaihay.com
|























Danh sách bình luận