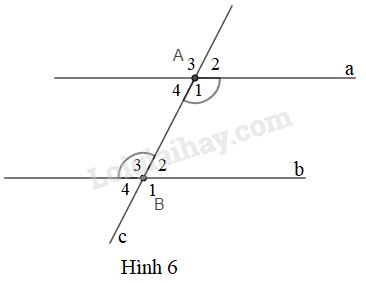
Phần câu hỏi bài 3 trang 91 Vở bài tập toán 7 tập 1

Câu 7.

Xem hình \(6\). Nếu có một cặp góc so le trong bằng nhau thì ta suy luận như thế nào để thấy hai góc trong cùng phía bù nhau?

Phương pháp giải:

Tổng số đo hai góc kề bù bằng \(180^o\)

Lời giải chi tiết:

Theo đề bài \(\widehat {{A_1}} = \widehat {{B_3}}\)     (1)

\(\widehat {{B_3}} + \widehat {{B_2}} = {180^o}\)  (vì \(\widehat {{B_3}}\)  và \(\widehat {{B_2}}\)  là  hai góc kề bù)     (2)

Từ (1) và (2) suy ra \(\widehat {{A_1}} + \widehat {{B_2}} = {180^o}\)

\(\widehat {{A_1}} + \widehat {{A_4}} = {180^o}\)  (vì \(\widehat {{A_1}}\)  và \(\widehat {{A_4}}\)  là hai góc kề bù)     (3)

Từ (1) và (3) suy ra \(\widehat {{B_3}} + \widehat {{A_4}} = {180^o}\)

Vậy một cặp góc so le trong bằng nhau thì ta suy ra hai góc trong cùng phía bù nhau.

Câu 8.

Xem hình \(6.\) Nếu có một cặp góc đồng vị bằng nhau thì ta suy luận như thé nào để thấy hai góc so le trong bằng nhau?

Phương pháp giải:

- Tổng số đo hai góc kề bù bằng \(180^o\).

- Hai góc đối đỉnh thì bằng nhau.

Lời giải chi tiết:

Giả sử có cặp góc đồng vị \(\widehat {{A_2}} = \widehat {{B_2}}\)     (1)

\(\widehat {{A_1}} + \widehat {{A_2}} = {180^o}\) (hai góc kề bù)           (2)

\(\widehat {{B_2}} + \widehat {{B_3}} = {180^o}\) (hai góc kề bù)           (3)

Từ (1), (2) và (3) suy ra \(\widehat {{A_1}} = \widehat {{B_3}}\)

\(\widehat {{A_2}} = \widehat {{A_4}}\)  (hai góc đối đỉnh)                  (4)

Từ (1) và (4) suy ra \(\widehat {{A_4}} = \widehat {{B_2}}\).

Câu 9.

Xem hình \(6.\) Hãy khoanh tròn vào chữ cái trước câu sai:

\(\begin{array}{l}a)\,\widehat {{A_4}} = \widehat {{B_2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b)\,\widehat {{A_1}} + \widehat {{B_2}} = {180^o}\\c)\,\widehat {{A_4}} = \widehat {{B_3}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,d)\,\widehat {{A_1}} = \widehat {{B_1}}\end{array}\)

Phương pháp giải:

Nếu đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\), trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:

- Hai góc so le trong còn lại bằng nhau.

- Hai góc đồng vị bằng nhau.

- Hai góc trong cùng phía bù nhau.

Lời giải chi tiết:

a) Đúng vì \(\widehat {{A_4}};\widehat {{B_2}}\)  là hai góc so le trong.

b) Đúng vì \(\widehat {{A_1}};\widehat {{B_2}}\)  là hai góc trong cùng phía.

c) Sai vì \(\widehat {{A_4}};\widehat {{B_3}}\) là hai góc trong cùng phía.

d) Đúng vì \(\widehat {{A_1}};\widehat {{B_1}}\)  là hai góc đồng vị.

Chọn c.

Loigiaihay.com