Bài 12 trang 91 Vở bài tập toán 7 tập 1

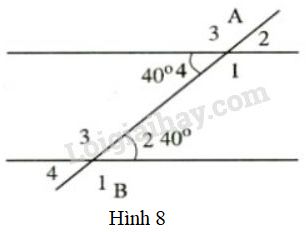
Đề bài

(Xem hình \(8\))

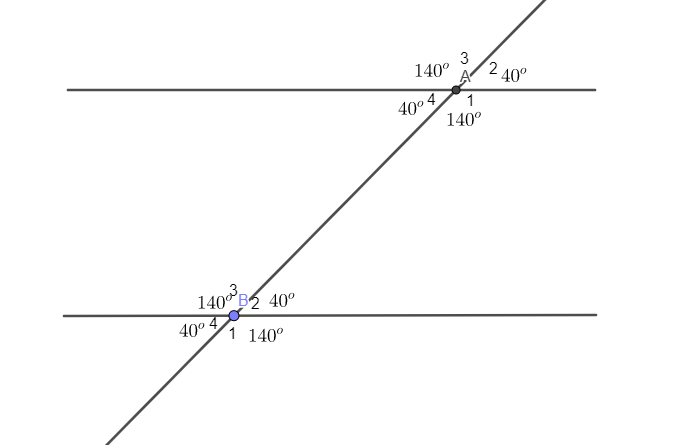
a) Ghi tiếp số đo ứng với các góc còn lại.

b) Cặp góc \(A_{1},B_{2}\) và cặp góc \(A_{4},B_{3}\) được gọi là hai cặp góc trong cùng phía.

Tính:

\(\widehat{A_{1}}+\widehat{B_{2}}; \widehat{A_{4}}+\widehat{B_{3}}\).

Lời giải chi tiết

a) \(\widehat {{A_2}} = \widehat {{A_4}}\) (Hai góc đối đỉnh) 

\( \Rightarrow \widehat {{A_2}} = {40^o}\)

\(\eqalign{
& \widehat {{A_1}} + \widehat {{A_4}} = {180^o}(\text{ hai góc kề bù }) \cr 
& \Rightarrow \widehat {{A_1}} = {180^0} - \widehat {{A_4}} \cr&\;\;\;\;\;\;\;\;\;\;= {180^o} - {40^o} = {140^o} \cr} \)

\(\eqalign{
& \widehat {{A_1}} = \widehat {{A_3}}(\text{ hai góc đối đỉnh }) \cr 
& \Rightarrow \widehat {{A_3}} = {140^o} \cr} \)

\(\eqalign{
& \widehat {{B_2}} = \widehat {{B_4}}(\text{ hai góc đối đỉnh }) \cr 
& \Rightarrow \widehat {{B_4}} = {40^o} \cr} \)

\(\eqalign{
& \widehat {{B_2}} + \widehat {{B_3}} = {180^o} (\text{ hai góc kề bù })\cr 
& \Rightarrow \widehat {{B_3}} = {180^o} - \widehat {{B_2}} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^o} - {40^o} = {140^o} \cr} \)

\(\eqalign{
& \widehat {{B_3}} = \widehat {{B_1}}(\text{ hai góc đối đỉnh }) \cr 
& \Rightarrow \widehat {{B_1}} = {140^o} \cr} \)

Ghi số đo ứng với các góc còn lại ta được hình bên:

b) Ta có:

\(\widehat{A_{1}}+\widehat{B_{2}}=140^{\circ}+40^{\circ}=180^{\circ}\)

\(\widehat{A_{4}}+\widehat{B_{3}}=40^{\circ}+140^{\circ}=180^{\circ}\).

Loigiaihay.com