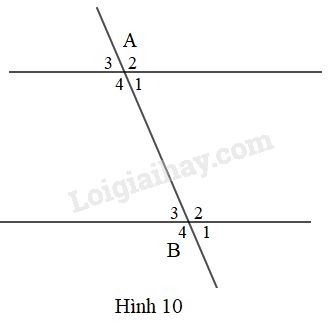
Bài 15 trang 92 Vở bài tập toán 7 tập 1Giải bài 15 trang 92 VBT toán 7 tập 1. Xem hình 10 . Ta gọi hai cặp góc so le ngoài là góc A_2 và góc B_4 ... Quảng cáo
Đề bài Xem hình \(10\) Ta gọi hai cặp góc so le ngoài là \(\widehat {{A_2}}\) và \(\widehat {{B_4}}\); \(\widehat {{A_3}}\) và \(\widehat {{B_1}}\). a) Vì sao nếu \(\widehat {{A_1}} = \widehat {{B_3}}\) thì \(\widehat {{A_2}}=\widehat {{B_4}}; \widehat {{A_3}}=\widehat {{B_1}}\) b) Phát biểu kết quả ở câu a) bằng lời.
Phương pháp giải - Xem chi tiết Sử dụng lí thuyết các góc tạo bởi một đường thẳng cắt hai đường thẳng - Hai góc kề bù là hai góc có chung \(1\) cạnh và \(2\) cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ là cạnh chung; tổng số đo hai góc đó bằng \(180^o\). - Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia. Lời giải chi tiết a) \(\widehat {{A_1}} + \widehat {{A_2}} = {180^o}\) (hai góc kề bù) \( \Rightarrow \widehat {{A_2}} = {180^o} - \widehat {{A_1}}\) (1) \(\widehat {{B_3}} + \widehat {{B_4}} = {180^o}\) (hai góc kề bù) \( \Rightarrow \widehat {{B_4}} = {180^o} - \widehat {{B_3}}\) (2) Mặt khác \(\widehat {{A_1}} = \widehat {{B_3}}\) (3) Từ (1), (2) và (3) suy ra: \(\widehat {{A_2}}=\widehat {{B_4}}\). \(\widehat {{A_1}} = \widehat {{A_3}}\) (hai góc đối đỉnh) (4) \(\widehat {{B_1}} = \widehat {{B_3}}\) (hai góc đối đỉnh) (5) Từ (3), (4) và (5) suy ra: \(\widehat {{A_3}}=\widehat {{B_1}}\). b) Nếu hai góc so le trong bằng nhau thì hai góc so le ngoài cũng bằng nhau. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
