Giải mục I trang 84, 85 SGK Toán 7 tập 2 - Cánh diều

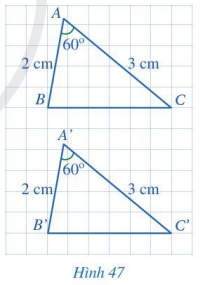
HĐ 2

Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A'} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?

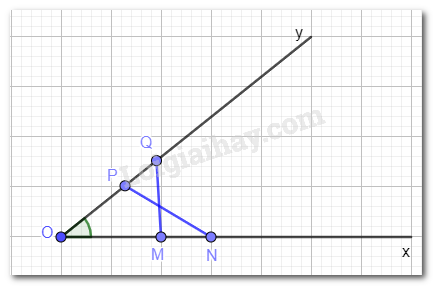
Phương pháp giải:

Đếm số ô vuông rồi so sánh BC và B’C’. Từ đó so sánh hai tam giác ABC và A’B’C’.

Lời giải chi tiết:

BC = B’C’ = 6 (ô vuông).

Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)

LT -VD 1

Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.

Phương pháp giải:

Chứng minh tam giác OMQ bằng tam giác OPN. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.

Lời giải chi tiết:

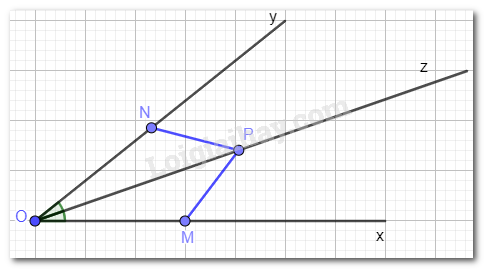
Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.

Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)

\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)

LT - VD 2

Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.

Phương pháp giải:

Muốn chứng minh MP = NP, ta chứng minh tam giác MOP bằng tam giác NOP.

Lời giải chi tiết:

Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)

\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)