Giải mục 4 trang 79, 80 SGK Toán 12 tập 1 - Cánh diều

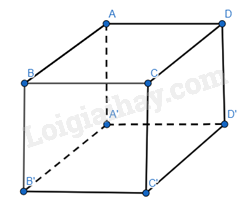
HĐ4

Trả lời câu hỏi Hoạt động 4 trang 79 SGK Toán 12 Cánh diều

a) Cho hình lập phương ABCD.A’B’C’D’ có A(0;0;0), B(1;0;0), D(0;1;0), C’(1;1;1). Hãy chỉ ra tọa độ của một vecto vuông góc với cả hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \)

b) Cho hai vecto \(\overrightarrow u  = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v  = ({x_2};{y_2};{z_2})\) không cùng phương. Xét vecto \(\overrightarrow w  = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\).

- Tính \(\overrightarrow w .\overrightarrow u \), \(\overrightarrow w .\overrightarrow v \)

- Vecto \(\overrightarrow w \) có vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) hay không?

Phương pháp giải:

Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\), ta có biểu thức tọa độ của tích vô hướng \(\overrightarrow a .\overrightarrow b  = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\) và \(\overrightarrow a  \bot \overrightarrow b  \Leftrightarrow \overrightarrow a .\overrightarrow b  = 0\).

Lời giải chi tiết:

a)

Ta có: \(\overrightarrow {AB}  = (1;0;0)\), \(\overrightarrow {AD}  = (0;1;0)\).

\(A'(0;0;1) \Rightarrow \overrightarrow {AA'}  = (0;0;1)\).

Ta có: \(\overrightarrow {AA'} .\overrightarrow {AB}  = 0.1 + 0.0 + 1.0 = 0 \Leftrightarrow \overrightarrow {AA'}  \bot \overrightarrow {AB} \).

\(\overrightarrow {AA'} .\overrightarrow {AD}  = 0.0 + 0.1 + 1.0 = 0 \Leftrightarrow \overrightarrow {AA'}  \bot \overrightarrow {AD} \).

Vậy \(\overrightarrow {AA'} \) vuông góc với cả hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \).

b) \(\overrightarrow w .\overrightarrow u  = ({y_1}{z_2} - {y_2}{z_1}){x_1} + ({z_1}{x_2} - {z_2}{x_1}){y_1} + ({x_1}{y_2} - {x_2}{y_1}){z_1}\)

\(= {x_1}{y_1}{z_2} - {x_1}{y_2}{z_1} + {y_1}{z_1}{x_2} - {y_1}{z_2}{x_1} + {z_1}{x_1}{y_2} - {z_1}{x_2}{y_1} = 0\).

\(\overrightarrow w .\overrightarrow v  = ({y_1}{z_2} - {y_2}{z_1}){x_2} + ({z_1}{x_2} - {z_2}{x_1}){y_2} + ({x_1}{y_2} - {x_2}{y_1}){z_2} \)

\(= {x_2}{y_1}{z_2} - {x_2}{y_2}{z_1} + {y_2}{z_1}{x_2} - {y_2}{z_2}{x_1} + {z_2}{x_1}{y_2} - {z_2}{x_2}{y_1} = 0\).

Vậy vecto \(\overrightarrow w \) có vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \).

LT4

Trả lời câu hỏi Luyện tập 4 trang 80 SGK Toán 12 Cánh diều

Trong không gian với hệ tọa độ Oxyz, cho hai vecto \(\overrightarrow u  = (1;0; - 3)\) và \(\overrightarrow v  = (0;0;3)\). Hãy chỉ ra tọa độ của một vecto \(\overrightarrow w \) khác \(\overrightarrow 0 \) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \).

Phương pháp giải:

Sử dụng công thức tính tích có hướng.

Lời giải chi tiết:

\(\overrightarrow w  = \left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 3}\\0&3\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 3}&1\\3&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&0\\0&0\end{array}} \right|} \right)\)

\((0.3 - 0.( - 3); - 3.0 - 3.1;1.0 - 0.0) = (0; - 3;0)\).

Vậy \(\overrightarrow w  = (0;3;0)\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \).