Giải mục 4 trang 21 SGK Toán 8 tập 1– Chân trời sáng tạoSử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
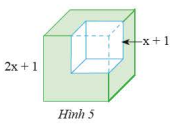
HĐ4 Video hướng dẫn giải Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở: \(\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) Phương pháp giải: Áp dụng quy tắc chuyển vế, các tính chất của phép toán, hằng đẳng thức: Bình phương của một tổng, một hiệu. Lời giải chi tiết: \(\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left[ {{a^2} + 2ab + {b^2} - 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left[ {{{\left( {a - b} \right)}^2} + 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left[ {{a^2} - 2ab + {b^2} + 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\end{array}\) Thực hành 7 Video hướng dẫn giải Viết các đa thức sau dưới dạng tích: a) \(8{y^3} + 1\) b) \({y^3} - 8\) Phương pháp giải: Biến đổi đa thức về dạng tổng, hiệu của hai lập phương rồi áp dụng hằng đẳng thức tổng, hiệu của hai lập phương. Lời giải chi tiết: a) \(8{y^3} + 1 = {\left( {2y} \right)^3} + {1^3} = \left( {2y + 1} \right)\left[ {{{\left( {2y} \right)}^2} - 2y.1 + {1^2}} \right] = \left( {2y + 1} \right)\left( {4{y^2} - 2y + 1} \right)\) b) \({y^3} - 8 = {y^3} - {2^3} = \left( {y - 2} \right)\left( {{y^2} + 2y + {2^2}} \right) = \left( {y - 2} \right)\left( {{y^2} + 2y + 4} \right)\) Thực hành 8 Video hướng dẫn giải Tính: a) \(\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\) b) \(\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right)\) Phương pháp giải: Biến đổi tích của hai đa thức về dạng vế phải của hằng đẳng thức: Tổng, hiệu của hai lập phương. Lời giải chi tiết: a) \(\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = \left( {x + 1} \right)\left( {{x^2} - x.1 + {1^2}} \right) = {x^3} + {1^3} = {x^3} + 1\) b) \(\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right) = \left( {2x - \dfrac{1}{2}} \right)\left[ {{{\left( {2x} \right)}^2} + 2x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2}} \right] = {\left( {2x} \right)^3} - {\left( {\dfrac{1}{2}} \right)^3} = 8{x^3} - \dfrac{1}{8}\) Vận dụng 4 Video hướng dẫn giải Từ một khối lập phương có cạnh bằng \(2x + 1\), ta cắt bỏ một khối lập phương có cạnh bằng \(x + 1\) (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức. Phương pháp giải: Áp dụng công thức tính thể tích của hình lập phương Áp dụng hằng đẳng thức: Hiệu của hai lập phương Lời giải chi tiết: Thể tích phần còn lại của khối lập phương là: \(\begin{array}{l}{\left( {2x + 1} \right)^3} - {\left( {x + 1} \right)^3}\\ = \left[ {\left( {2x + 1} \right) - \left( {x + 1} \right)} \right].\left[ {{{\left( {2x + 1} \right)}^2} + \left( {2x + 1} \right)\left( {x + 1} \right) + {{\left( {x + 1} \right)}^2}} \right]\\ = x.\left[ {4{x^2} + 4x + 1 + 2{x^2} + 2x + x + 1 + {x^2} + 2x + 1} \right]\\ = x.\left( {7{x^2} + 9x + 3} \right)\\ = 7{x^3} + 9{x^2} + 3x\end{array}\)
|




















Danh sách bình luận